练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    （1）证明：∵，    

    ∴．    …………………………………………（2分）

    ∵，      …………………………………………（1分）

    ∴∽．……………………………………… （1分）

    ∴． ……………………………………………（1分）

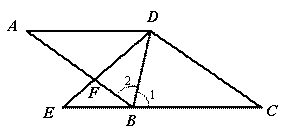
           （2）   ∵，

    又∵，

      ∴．………………………………………………（1分）

    ∴．       ………………………………………………（1分）

    又∵，

    ∴四边形是平行四边形 ………………………………………（1分）

    ∵，

    ∴．       ……………………………………………（1分）

    ∵平分，

    ∴．            …………………………………………（1分）

    ∴．

    ∴．        ……………………………………………（1分）

    ∴四边形是菱形．   ……………………………………………………（1分）

    已知正方形ABCD的边长为4，E是CD上一个动点，以CE为一条直角边作等腰直角三角形CEF，连结BF、BD、FD．

    （1）BD与CF的位置关系是                 ．

    （2）①如图1，当CE=4（即点E与点D重合）时，△BDF的面积为          ．

    ②如图2，当CE=2（即点E为CD的中点）时，△BDF的面积为          ．

    ③如图3，当CE=3时，△BDF的面积为          ．

     


    （3）如图4，根据上述计算的结果，当E是CD上任意一点时，请提出你对△BDF面积与正方形ABCD的面积之间关系的猜想，并证明你的猜想．

     


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    22、如图，已知：点B，F，C，D在同一直线上，且FB=CD，AB∥ED，AC∥FE，请你根据上述条件，判断∠A与∠E的大小关系，并给出证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

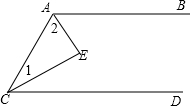    精英家教网如图，AB∥CD，AE平分∠BAC，CE平分∠ACD，求∠E为多少？
    下面是小明同学的解法，请帮助他完成证明．
    证明：因为∠1=∠ECD=
    1
    2
    ∠ACD （原因：
     
    ）
    又因为∠2=（∠BAE　　）=
    1
    2
    ∠CAB（原因：
     
    ）
    又因为AB∥CD，
    所以∠CAB+∠ACD=180°（原因：
     
    ）
    所以∠1+∠2=
    1
    2
    （∠CAB+∠ACD）=90°（等量代换）
    又因为∠1+∠2+∠E=180°（原因：
     
    ）
    所以∠E=90°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    对于正数x，规定f（x）=
    x2
    1+x2
    ，
    （1）计算f（2）=
     
    ；f（
    1
    2
    ）=
     
    ；f（2）+f（
    1
    2
    ）=
     
    ；f（3）+f（
    1
    3
    ）=
     
    ；…
    （2）猜想f（x）+f(
    1
    x
    )    =
     
    ，请予以证明．
    （3）现在你会计算f(
    1
    2010
    )    +f（
    1
    2009
    ）+f（
    1
    2008
    ）+f（
    1
    2007
    ）+f（
    1
    2006
    ）+…f（
    1
    3
    ）+f（
    1
    2
    ）+f（1）+f（2）+f（3）+…+f（2006）+f（2007）+f（2008）+f（2009）+f（2010）的值了吗，写出你的计算过程．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，已知在Rt△ABC中，∠B=90°，AC=13，AB=5，O是AB上的点，以O为圆心，OB精英家教网为半径作⊙O．
    （1）当OB=2.5时，⊙O交AC于点D，求CD的长；
    （2）当OB=2.4时，AC与⊙O的位置关系如何？试证明你的结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    20、如图，AE∥BC，AE平分∠CAD，试说明∠B=∠C
    证明：∵AE∥BC
    已知

    ∴∠1=
    ∠B（两直线平行，同位角相等）

    ∠2=
    ∠C（两直线平行，内错角相等）

    又∵AE平分∠CAD
    ∴∠1=∠2
    角平分线的定义

    ∴∠
    B
    =∠
    C
    ．

    查看答案和解析>>

    同步练习册答案