
【题目】(本题12分)如图甲,在平面直角坐标系中,直线y=![]() x+8分别交x轴、y轴于点A、B,⊙O的半径为2
x+8分别交x轴、y轴于点A、B,⊙O的半径为2![]() 个单位长度.点P为直线y=
个单位长度.点P为直线y=![]() x+8上的动点,过点P作⊙O的切线PC、PD,切点分别为C、D,且PC⊥PD.
x+8上的动点,过点P作⊙O的切线PC、PD,切点分别为C、D,且PC⊥PD.

(1)试说明四边形OCPD的形状(要有证明过程);
(2)求点P的坐标;
(3)如图乙,若直线y=![]() x+b将⊙O的圆周分成两段弧长之比为1:3,请直接写出b的值
x+b将⊙O的圆周分成两段弧长之比为1:3,请直接写出b的值
(4)向右移动⊙O(圆心O始终保持在x轴上),试求出当⊙O与直线y=![]() x+8有交点时圆心O的横坐标m的取值范围。
x+8有交点时圆心O的横坐标m的取值范围。
【答案】(1)四边形OCPD为正方形;
(2)求点P的坐标为(2,6)或(6,2);
(3)b的值为![]() ;
;
(4)m的取值范围为![]() .(直接写出答案)
.(直接写出答案)
【解析】
试题(1)根据切线长的性质定理可以得出PC=PD,PC⊥OC, PC⊥OD,再由PC⊥PD可以的证.
(2)设出直线y=![]() x+8的点P(m,-m+8),根据切线长的性质和正方形的性质,有勾股定理的出m的值.
x+8的点P(m,-m+8),根据切线长的性质和正方形的性质,有勾股定理的出m的值.
(3)分两种情形,直线y=-x+b将圆周分成两段弧长之比为1:3,可知被割得的弦所对的圆心角为90°,又直线y=-x+b与坐标轴的夹角为45°,如图乙可知,分两种情况,可求得结果.
(4)当圆运动到PO等于半径且在直线的左面时,则圆和直线有一个交点;当圆运动到直线的右面时与直线相切的点也有一个,从而能知道他们之间的都可以.
试题解析:(1)四边形OCPD是正方形.证明过程如下:
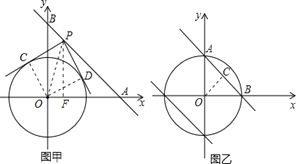
如图甲,连接OC、OD.
∵PC、PD是⊙O的两条切线,
∴∠PCO=∠PDO=90°.
又∵PC⊥PD,
∴四边形OCPD是矩形.
又∵OC=OD,
∴四边形OCPD是正方形;
(2)如图甲,过P作x轴的垂线,垂足为F,连接OP.
∵PC、PD是⊙O的两条切线,∠CPD=90°,
∴∠OPD=∠OPC=![]() ∠CPD=45°,
∠CPD=45°,
∵∠PDO=90°,∠POD=∠OPD=45°,
∴OD=PD=2![]() ,OP=2
,OP=2![]()
∵P在直线y=-x+8上,设P(m,-m+8),则OF=m,PF=-m+8,
∵∠PFO=90°,OF2+PF2=PO2,
∴m2+(-m+8)2=(2![]() )2,
)2,
解得m=2或6,
∴P的坐标为(2,6)或(6,2);
(3)分两种情形,直线y=-x+b将圆周分成两段弧长之比为1:3,可知被割得的弦所对的圆心角为90°,又直线y=-x+b与坐标轴的夹角为45°,如图乙可知,分两种情况,所以,b的值为2![]() 或-2
或-2![]() .
.
故答案是:2![]() 或-2
或-2![]() .
.
(4)8-2![]() ≤m≤8+2
≤m≤8+2![]()


 英才计划期末调研系列答案
英才计划期末调研系列答案 精英口算卡系列答案
精英口算卡系列答案科目:初中数学 来源: 题型:
【题目】如图,是我国第24~30届奥运奖牌数的回眸和中国代表团奖牌总数统计图,根据表和统计图,以下描述正确的是( )
金牌(块) | 银牌(块) | 铜牌(块) | 总计奖牌数 | |
24 | 5 | 11 | 12 | 28 |
25 | 16 | 22 | 12 | 54 |
26 | 16 | 22 | 12 | 50 |
27 | 28 | 16 | 15 | 59 |
28 | 32 | 17 | 14 | 63 |
29 | 51 | 21 | 28 | 100 |
30 | 38 | 27 | 23 | 88 |

A.中国代表团的奥运奖牌总数一直保持上升趋势
B.折线统计图中的六条线段只是为了便于观察图象所反映的变化,不表示某种意思
C.与第29届北京奥运会相比,奥运金牌数、银牌数、铜牌数都有所下降
D.评价一个代表团在一届奥运会上的表现,我们只需关注金牌数,无需考虑其他
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,AC=6,BC=8,D是AB上一动点,过点D作DE⊥AC于点E,DF⊥BC于点F,连接EF,则线段EF的最小值是( )

A. 4B. 4.6C. 4.8D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李大妈加盟了“红红”全国烧烤连锁店,该公司的宗旨是“薄利多销”,经市场调查发现,当羊肉串的单价定为![]() 元时,每天能卖出
元时,每天能卖出![]() 串,在此基础上,每加价
串,在此基础上,每加价![]() 元李大妈每天就会少卖出
元李大妈每天就会少卖出![]() 串,考虑了所有因素后李大妈的每串羊肉串的成本价为
串,考虑了所有因素后李大妈的每串羊肉串的成本价为![]() 元,若李大妈每天销售这种羊肉串想获得利润是
元,若李大妈每天销售这种羊肉串想获得利润是![]() 元,那么请问这种羊肉串应怎样定价?
元,那么请问这种羊肉串应怎样定价?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC为等边三角形,D为AC的中点,∠EDF=120°,DE交线段AB于E,DF交直线BC于F.
(1)如图(1),求证:DE=DF;
(2)如图(2),若BE=3AE,求证:CF=![]() BC.
BC.
(3)如图(3),若BE=![]() AE,则CF= BC;在图(1)中,若BE=4AE,则CF= BC.
AE,则CF= BC;在图(1)中,若BE=4AE,则CF= BC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,BC=2AB,对角线相交于O,过C点作CE⊥BD交BD于E点,H为BC中点,连接AH交BD于G点,交EC的延长线于F点,下列5个结论:①EH=AB;②∠ABG=∠HEC;③△ABG≌△HEC;④S△GAD=S四边形GHCE,⑤CF=BD.正确的有( )个.

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂在生产过程中要消耗大量电能,消耗每千度电产生利润与电价是一次函数关系,经过测算,工厂每千度电产生利润![]() (元/千度))与电价
(元/千度))与电价![]() (元/千度)的函数图象如图:
(元/千度)的函数图象如图:

![]() 当电价为
当电价为![]() 元/千度时,工厂消耗每千度电产生利润是多少?
元/千度时,工厂消耗每千度电产生利润是多少?
![]() 为了实现节能减排目标,有关部门规定,该厂电价
为了实现节能减排目标,有关部门规定,该厂电价![]() (元/千度)与每天用电量
(元/千度)与每天用电量![]() (千度)的函数关系为
(千度)的函数关系为![]() ,且该工厂每天用电量不超过
,且该工厂每天用电量不超过![]() 千度,为了获得最大利润,工厂每天应安排使用多少度电?工厂每天消耗电产生利润最大是多少元?
千度,为了获得最大利润,工厂每天应安排使用多少度电?工厂每天消耗电产生利润最大是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋子中装有大小、质地完全相同的4只小球,小球上分别标有1,2,3,4四个数字.
(1)从袋中随机摸出一只小球,求小球上所标数字为质数的概率;
(2)从袋中随机摸出一只小球,再从剩下的小球中随机摸出一只小球,求两次摸出的小球上所标数字之和为5的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com