
分析 先将原式进行变形,然后进行分解,再化简即可解答本题.
解答 解:$\frac{\frac{2}{{x}^{2}-1}+\frac{4}{{x}^{2}-4}+…+\frac{20}{{x}^{2}-100}}{\frac{1}{(x-1)(x+10)}+\frac{1}{(x-2)(x+9)}+…+\frac{1}{(x-10)(x+1)}}$
=$\frac{\frac{(x+1)-(x-1)}{(x+1)(x-1)}+\frac{(x+2)-(x-2)}{(x+2)(x-2)}+…+\frac{(x+10)-(x-10)}{(x+10)(x-10)}}{\frac{1}{11}[(\frac{1}{x-1}-\frac{1}{x+10})+(\frac{1}{x-2}-\frac{1}{x+9})+…+(\frac{1}{x-10}-\frac{1}{x+1})]}$
=$\frac{(\frac{1}{x-1}+\frac{1}{x-2}+…+\frac{1}{x-10})-(\frac{1}{x+1}+\frac{1}{x+2}+…+\frac{1}{x+10})}{\frac{1}{11}[(\frac{1}{x-1}+\frac{1}{x-2}+…+\frac{1}{x-10})-(\frac{1}{x+1}+\frac{1}{x+2}+…+\frac{1}{x+10})]}$
=11.
故答案为:11.
点评 本题考查分式的混合运算,解题的关键是巧妙的对分式的分子和分母进行分解.


科目:初中数学 来源: 题型:解答题
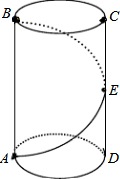 一只螳螂在一圆柱形松树树干的A点处,发现它的正上方B点处有一只小虫子,螳螂想捕到这只虫子,但又怕被发现,于是按如图所示的路线,绕到虫子后面吃掉它.已知树干的周长为20cm,A、B两点的距离为15cm.若螳螂想吃掉在B点的小虫子,求螳螂绕行的最短路程.
一只螳螂在一圆柱形松树树干的A点处,发现它的正上方B点处有一只小虫子,螳螂想捕到这只虫子,但又怕被发现,于是按如图所示的路线,绕到虫子后面吃掉它.已知树干的周长为20cm,A、B两点的距离为15cm.若螳螂想吃掉在B点的小虫子,求螳螂绕行的最短路程.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 若将三个数-$\sqrt{3}$,$\sqrt{6}$,$\sqrt{14}$表示在数轴上,其中能被如图所示的墨迹覆盖的数是$\sqrt{6}$.
若将三个数-$\sqrt{3}$,$\sqrt{6}$,$\sqrt{14}$表示在数轴上,其中能被如图所示的墨迹覆盖的数是$\sqrt{6}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在矩形ABCD中,E为边CD的中点,连接AE、BE、BE交AC于点O
如图,在矩形ABCD中,E为边CD的中点,连接AE、BE、BE交AC于点O查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,甲、乙两组同学去野外采集标本,他们从同一地点同时出发,各自沿固定的方向行走.当甲组行走600m、乙组行走630m时,两组的所在地相距870m,那么甲、乙两组同学行走的方向成多少度的角(即图中的α为多少度)?
如图,甲、乙两组同学去野外采集标本,他们从同一地点同时出发,各自沿固定的方向行走.当甲组行走600m、乙组行走630m时,两组的所在地相距870m,那么甲、乙两组同学行走的方向成多少度的角(即图中的α为多少度)?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图所示,△OA1B1,△A1A2B2,△A2A3B3,…,△An-1AnBn,都是等腰直角三角形,斜边OB1,A1B2,…,An-1Bn的中点P1(x1,y1),P2(x2,y2),…,Pn(xn,yn)都在函数$y=\frac{16}{x}(x>0)$的图象上,则y1+y2+y3+…+yn=4$\sqrt{n}$.
如图所示,△OA1B1,△A1A2B2,△A2A3B3,…,△An-1AnBn,都是等腰直角三角形,斜边OB1,A1B2,…,An-1Bn的中点P1(x1,y1),P2(x2,y2),…,Pn(xn,yn)都在函数$y=\frac{16}{x}(x>0)$的图象上,则y1+y2+y3+…+yn=4$\sqrt{n}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com