
【题目】如图,直线y=x﹣4与x轴、y轴分别交于M、N两点,以坐标原点O为圆心的⊙O半径为2,将⊙O沿x轴向右平移,当⊙O恰好与直线MN相切时,平移的最小距离为 . 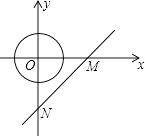
【答案】4﹣2 ![]()
【解析】解:如图,设⊙O′与直线MN相切于点H.
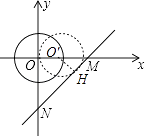
由题意OM=ON=4,∠OMN=45°
在Rt△O′HM中,∵O′H=2,
∴O′M=2 ![]() ,
,
∴OO′=4﹣2 ![]() ,
,
∴当⊙O恰好与直线MN相切时,平移的最小距离为4﹣2 ![]() .
.
【考点精析】本题主要考查了切线的性质定理和解直角三角形的相关知识点,需要掌握切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径;解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法)才能正确解答此题.


科目:初中数学 来源: 题型:
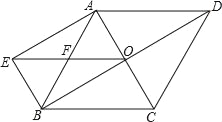
【题目】如图,菱形ABCD对角线交于点O,BE∥AC,AE∥BD,EO与AB交于点F.
(1)求证:EO=DC;
(2)若菱形ABCD的边长为10,∠EBA=60°,求:菱形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场在一楼与二楼之间装有一部自动扶梯,以均匀的速度向上行驶,一男孩与一女孩同时从自动扶梯上走到二楼(扶梯本身也在行驶).如果二人都做匀速运动,且男孩每分钟走动的级数是女孩的两倍.又已知男孩走了27级到达顶部,女孩走了18级到达顶部(二人每步都只跨1级).求扶梯有多少级?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请完成下面的解答过程.
如图,∠1=∠B,∠C=110°,求∠3的度数.
解:∵∠1=∠B,
∴AD∥ .( )
∴∠C+ =180°.(两直线平行,同旁内角互补)
∵∠C=110°,
∴∠2= °.
∴∠3= =70°.( )

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习三角形中位线的性质时,小亮对课本给出的解决办法进行了认真思考:
课本研究三角形中位线性质的方法 |

请你利用小亮的发现解决下列问题:
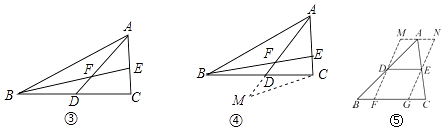
(1)如图③,AD是△ABC的中线,BE交AC于点E,交AD于点F,且AE=EF,求证:AC=BF.
请你帮助小亮写出辅助线作法并完成论证过程:
(2)解决问题:如图⑤,在△ABC中,∠B=45°,AB=10,BC=8,DE是△ABC的中位线.过点D,E作DF∥EG,分别交BC于点F,G,过点A作MN∥BC,分别与FD,GE的延长线交于点M,N,则四边形MFGN周长的最小值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AC=6,BC=8,AB=10,∠BCA的平分线与AB的垂直平分线DG交于点D,DE⊥CA的延长线于点E,DF⊥CB于点F.
(1)判断△ABC的形状,并说明理由;
(2)求证:AE=BF;
(3)求DG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给出下列判断:
①若|﹣a|=a,则a<0;
②有理数包括整数、0和分数;
③任何正数都大于它的倒数;
④2ax2﹣xy+y2是三次三项式;
⑤几个有理数相乘,当负因数的个数是奇数时,积一定为负.
上述判断正确的有( )
A. 0个B. 1个C. 2个D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,已知△ABC,

(1)分别画出与△ABC关于x轴、y轴对称的图形△A1B1C1和△A2B2C2;
(2)写出△A1B1C1和△A2B2C2各顶点坐标;
(3)求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com