
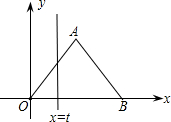
 如图,在直角坐标系中,正△AOB的边长为2,设直线x=t(0≤t≤2)截这个三角形所得位于此直线左方的图形的面积为y,则y关于t的函数图象大致是( )
如图,在直角坐标系中,正△AOB的边长为2,设直线x=t(0≤t≤2)截这个三角形所得位于此直线左方的图形的面积为y,则y关于t的函数图象大致是( )| A. | 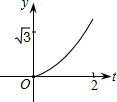 | B. | 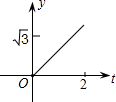 | C. | 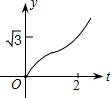 | D. | 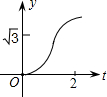 |
分析 ①0≤t≤1时,等边△AOB中,l∥y轴,所以很容易求得∠OCD=30°;进而证明OD=t,CD=$\sqrt{3}$t;最后根据三角形的面积公式,解答出y与t之间的函数关系式;
②1<t≤2时,可得BD=2-t,CD=$\sqrt{3}$(2-t),根据所截图形面积=S△OAB-S△BCD可得y与t的函数关系式,根据两个关系式可判断图象.
解答 解:①∵l∥y轴,△AOB为等边三角形,
∴∠OCD=30°,
∴OD=t,CD=$\sqrt{3}$t;
∴S△OCD=$\frac{1}{2}$×OD×CD
=$\frac{\sqrt{3}}{2}$t2(0≤t≤1),
即y=$\frac{\sqrt{3}}{2}$t2(0≤t≤1).
故此时y与t之间的函数关系的图象应为开口向上的二次函数图象;
②∵l∥y轴,△AOB为等边三角形
∴∠CBD=30°,
∴BD=2-t,CD=$\sqrt{3}$(2-t);
∴S△BCD=$\frac{1}{2}$×BD×CD=$\frac{\sqrt{3}}{2}$(2-t)2(1<t≤2),
即y=$\sqrt{3}$-$\frac{\sqrt{3}}{2}$(2-t)2(1<t≤2).
故此时y与t之间的函数关系的图象应为开口向下的二次函数图象,
故选:D.
点评 本题主要考查的是二次函数解析式的求法及二次函数的图象特征,根据直线的运动情况分类讨论并会求所截部分面积是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
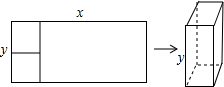 如图,在矩形中截取两个相同的正方形作为长方体的上、下底面,剩余的矩形恰好作为长方体的侧面,设原矩形的长和宽分别为x、y,则y与x的函数图象大致是( )
如图,在矩形中截取两个相同的正方形作为长方体的上、下底面,剩余的矩形恰好作为长方体的侧面,设原矩形的长和宽分别为x、y,则y与x的函数图象大致是( )| A. | 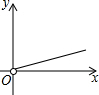 | B. | 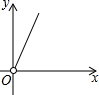 | C. | 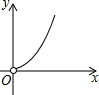 | D. | 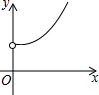 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2$\sqrt{3}$+4$\sqrt{2}$=6$\sqrt{5}$ | B. | $\sqrt{{(-5)}^{2}}$=-5 | C. | 3$\sqrt{3}$+3$\sqrt{2}$=3$\sqrt{6}$ | D. | $\sqrt{27}$÷$\sqrt{3}$=3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 总体 | B. | 样本 | C. | 个体 | D. | 样本容量 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com