
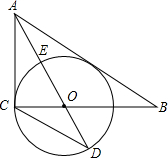
 如图,在Rt△ABC中,∠ACB=90°,AO是△ABC的角平分线.以O为圆心,OC为半径作⊙O.
如图,在Rt△ABC中,∠ACB=90°,AO是△ABC的角平分线.以O为圆心,OC为半径作⊙O.分析 (1)由于题目没有说明直线AB与⊙O有交点,所以过点O作OF⊥AB于点F,然后证明OC=OF即可;
(2)连接CE,先求证∠ACE=∠ODC,然后可知△ACE∽△ADC,所以$\frac{AE}{AC}=\frac{CE}{CD}$,而tan∠D=$\frac{CE}{CD}$=$\frac{1}{2}$;
(3)由(2)可知,AC2=AE•AD,所以可求出AE和AC的长度,由(1)可知,△OFB∽△ABC,所以$\frac{BF}{BC}=\frac{OF}{AC}$,然后利用勾股定理即可求得AB的长度.
解答 (1)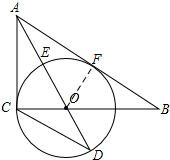 如图,过点O作OF⊥AB于点F,
如图,过点O作OF⊥AB于点F,
∵AO平分∠CAB,
OC⊥AC,OF⊥AB,
∴OC=OF,
∴AB是⊙O的切线;
(2)如图,连接CE,
∵ED是⊙O的直径,
∴∠ECD=90°,
∴∠ECO+∠OCD=90°,
∵∠ACB=90°,
∴∠ACE+∠ECO=90°,
∴∠ACE=∠OCD,
∵OC=OD,
∴∠OCD=∠ODC,
∴∠ACE=∠ODC,
∵∠CAE=∠CAE,
∴△ACE∽△ADC,
∴$\frac{AE}{AC}=\frac{CE}{CD}$,
∵tan∠D=$\frac{1}{2}$,
∴$\frac{CE}{CD}$=$\frac{1}{2}$,
∴$\frac{AE}{AC}$=$\frac{1}{2}$;
(3)由(2)可知:$\frac{AE}{AC}$=$\frac{1}{2}$,
∴设AE=x,AC=2x,
∵△ACE∽△ADC,
∴$\frac{AE}{AC}=\frac{AC}{AD}$,
∴AC2=AE•AD,
∴(2x)2=x(x+6),
解得:x=2或x=0(不合题意,舍去),
∴AE=2,AC=4,
由(1)可知:AC=AF=4,
∠OFB=∠ACB=90°,
∵∠B=∠B,
∴△OFB∽△ACB,
∴$\frac{BF}{BC}$=$\frac{OF}{AC}$,
设BF=a,
∴BC=$\frac{4a}{3}$,
∴BO=BC-OC=$\frac{4a}{3}$-3,
在Rt△BOF中,
BO2=OF2+BF2,
∴($\frac{4a}{3}$-3)2=32+a2,
∴解得:a=$\frac{72}{7}$或a=0(不合题意,舍去),
∴AB=AF+BF=$\frac{100}{7}$.
点评 本题考查圆的综合问题,解题的关键是证明△ACE∽△ADC.本题涉及勾股定理,解方程,圆的切线判定知识,内容比较综合,需要学生构造辅助线才能解决问题,对学生综合能力要求较高.


科目:初中数学 来源: 题型:填空题
 在一次寻宝游戏中,寻宝人找到了如图所示的两个标志,点A(2,3)、B(4,1),这两个标志点到“宝藏”点的距离都是2,则“宝藏”点的坐标是(2,1)和(4,3).
在一次寻宝游戏中,寻宝人找到了如图所示的两个标志,点A(2,3)、B(4,1),这两个标志点到“宝藏”点的距离都是2,则“宝藏”点的坐标是(2,1)和(4,3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,在正方形ABCD中,点E、F分别在边BC和CD上,∠BAE=∠DAF.联结AC交EF于点O,延长OC至点M,联结EM、FM.
已知:如图,在正方形ABCD中,点E、F分别在边BC和CD上,∠BAE=∠DAF.联结AC交EF于点O,延长OC至点M,联结EM、FM.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
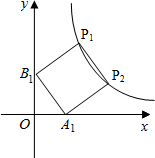 如图,正方形A1B1P1P2顶点P1、P2在反比例函数y=$\frac{2}{x}$(x>0)的图象上,顶点A1、B1分别在x轴、y轴的正半轴上,则点P2的坐标为(2,1).
如图,正方形A1B1P1P2顶点P1、P2在反比例函数y=$\frac{2}{x}$(x>0)的图象上,顶点A1、B1分别在x轴、y轴的正半轴上,则点P2的坐标为(2,1).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com