
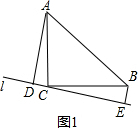
 解:分为两种情况:
解:分为两种情况:
|
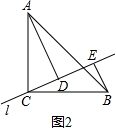
|


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
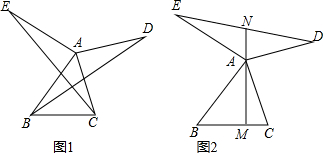 如图1,AB=AE,AC=AD,∠BAE=∠CAD=90°.
如图1,AB=AE,AC=AD,∠BAE=∠CAD=90°.查看答案和解析>>
科目:初中数学 来源: 题型:
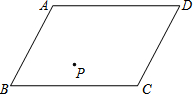 解决问题:有兄弟俩分家时,原来共同承包的一块平行四边形田地ABCD,现要进行平均划分,由于在这块地里有一口水井P,如图所示,为了兄弟俩都能方便使用这口井,兄弟俩在划分时犯难了.聪明的你能帮他们解决这个问题吗?
解决问题:有兄弟俩分家时,原来共同承包的一块平行四边形田地ABCD,现要进行平均划分,由于在这块地里有一口水井P,如图所示,为了兄弟俩都能方便使用这口井,兄弟俩在划分时犯难了.聪明的你能帮他们解决这个问题吗?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com