
【题目】同学们,我们知道图形是由点、线、面组成,结合具体实例,已经感受到“点动成线,线动成面”的现象,下面我们一起来进一步探究:
(概念认识)
已知点P和图形M,点B是图形M上任意一点,我们把线段PB长度的最小值叫做点P与图形M之间的距离.
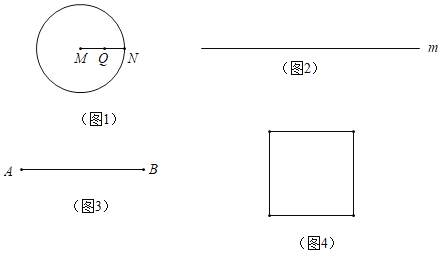
例如,以点M为圆心,1cm为半径画圆如图1,那么点M到该圆的距离等于1cm;若点N是圆上一点,那么点N到该圆的距离等于0cm;连接MN,若点Q为线段MN中点,那么点Q到该圆的距离等于0.5cm,反过来,若点P到已知点M的距离等于1cm,那么满足条件的所有点P就构成了以点M为圆心,1cm为半径的圆.
(初步运用)
(1)如图2,若点P到已知直线m的距离等于1cm,请画出满足条件的所有点P.
(深入探究)
(2)如图3,若点P到已知线段的距离等于1cm,请画出满足条件的所有点P.
(3)如图4,若点P到已知正方形的距离等于1cm,请画出满足条件的所有点P.
【答案】【初步运用】(1)见解析;【深入探究】(2)见解析;(3)见解析;
【解析】
(1)由题意可知:满足条件的所有的点P是平行于直线m且到直线m距离为1cm的两条直线,据此解答即可;
(2)由题意可知:满足条件的所有的点P是平行于线段AB且到线段AB距离为1cm的两条线段和以点A与点B为圆心,1cm为半径的两个半圆,据此解答即可;
(3)由题意可知:满足条件的所有的点P是平行于正方形其中一条边且到其中一边的距离为1cm的八条线段和以正方形的四个顶点为圆心,1cm为半径的四个四分之一圆,据此解答即可.
解:【初步运用】
(1)∵点P到已知直线m的距离等于1cm,
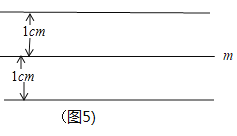
∴满足条件的所有的点P是平行于直线m且到直线m距离为1cm的两条直线,如图(5)所示:
【深入探究】
(2)∵点P到已知线段的距离等于1cm,
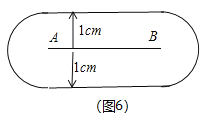
∴满足条件的所有的点P是平行于线段AB且到线段AB距离为1cm的两条线段和以点A与点B为圆心,1cm为半径的两个半圆,如图(6)所示,
(3)∵点P到已知正方形的距离等于1cm,
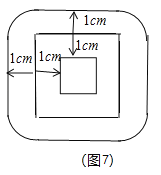
∴满足条件的所有的点P是平行于正方形其中一条边且到其中一边的距离为1cm的八条线段和以正方形的四个顶点为圆心,1cm为半径的四个四分之一圆,如图7所示,


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,将四张边长各不相同的正方形纸片按如图方式放入矩形ABCD内(相邻纸片之间互不重叠也无缝隙),未被四张正方形纸片覆盖的部分用阴影表示,设右上角与左下角阴影部分的周长的差为l.若知道l的值,则不需要测量就能知道周长的正方形的标号为( )

A.①B.②C.③D.④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文化用品商店用1 000元购进一批“晨光”套尺,很快销售一空;商店又用1 500元购进第二批该款套尺,购进时单价是第一批的![]() 倍,所购数量比第一批多100套.
倍,所购数量比第一批多100套.
(1)求第一批套尺购进时单价是多少?
(2)若商店以每套4元的价格将这两批套尺全部售出,可以盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
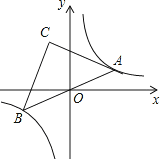
【题目】如图,点A是双曲线y=![]() 在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为 .
在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC在平面直角坐标系xOy中的位置如图所示.
(1)作△ABC关于点C成中心对称的△A1B1C1;
(2)将△A1B1C1向右平移3个单位,作出平移后的△A2B2C2;
(3)在x轴上求作一点P,使PA1+PC2的值最小,并求最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+3(a≠0)经过点A(﹣1,0),B(![]() ,0),且与y轴相交于点C.
,0),且与y轴相交于点C.
(1)求这条抛物线的表达式;
(2)求∠ACB的度数;
(3)设点D是所求抛物线第一象限上一点,且在对称轴的右侧,点E在线段AC上,且DE⊥AC,当△DCE与△AOC相似时,求点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从数轴上的原点开始,先向左移动2cm到达A点,再向左移动4cm到达B点,然后向右移动10cm到达C点.
![]()
(1)用1个单位长度表示1cm,请你在题中所给的数轴上表示出A、B、C三点的位置;
(2)把点C到点A的距离记为CA,则CA=______cm;
(3)若点B以每秒3cm的速度向左移动,同时A、C点以每秒lcm、5cm的速度向右移动,设移动时间为t(t>0)秒,试探究CA﹣AB的值是否会随着t的变化而改变?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于有理数a,b,定义一种新运算“⊙”,规定a⊙b=|a+b|+|a﹣b|.
![]()
(1)计算2⊙(﹣3)的值;
(2)当a,b在数轴上的位置如图所示时,化简a⊙b;
(3)已知(a⊙a)⊙a=8+a,求a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com