
 如图,王海同学为了测量校园内一棵大树EF的高度,他走到了校园的围墙CD外(如图所示),然后他沿着过点F与墙CD垂直的直线从远处向围墙靠近至B处,使大树恰好被围墙挡住顶端C和树的顶端E时,三点在同一条直线上.若BD=2米,CD=3米,FD=8米,王海身高1.6米.求大树的高度.
如图,王海同学为了测量校园内一棵大树EF的高度,他走到了校园的围墙CD外(如图所示),然后他沿着过点F与墙CD垂直的直线从远处向围墙靠近至B处,使大树恰好被围墙挡住顶端C和树的顶端E时,三点在同一条直线上.若BD=2米,CD=3米,FD=8米,王海身高1.6米.求大树的高度. 分析 作AH⊥EF于H,交CD于G,则AG=BD=2,GH=DF=8,AB=DG=HF=1.6,CG=CD-DG=3-1.6=1.4,证明△AGC∽△AHE,利用相似比计算出EH,然后计算EH+FH即可.
解答 解:如图,作AH⊥EF于H,交CD于G,则AG=BD=2,GH=DF=8,AB=DG=HF=1.6,CG=CD-DG=3-1.6=1.4,
∵CG∥EH,
∴△AGC∽△AHE,
∴$\frac{CG}{EH}$=$\frac{AG}{AH}$,即$\frac{1.4}{EH}$=$\frac{2}{2+8}$,
∴EH=7,
∴EF=EH+HF=7+1.6=8.6(m).
答:大树的高度为8.6米.
点评 本题考查了相似三角形的应用:利用杆或直尺测量物体的高度就是利用杆或直尺的高(长)作为三角形的边,利用视点和盲区的知识构建相似三角形,用相似三角形对应边的比相等的性质求物体的高度.


科目:初中数学 来源: 题型:选择题
| A. | 0,1,2,3 | B. | 0,1,2 | C. | -1,1,2,3 | D. | 1,2,3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
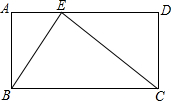 如图,∠A=∠D=90°,AB=CD=12cm,AD=BC=25cm,点E是AD上一点,且AE=9cm,连接BE,CE.判断∠BEC的锐角、钝角还是直角,并说明理由.
如图,∠A=∠D=90°,AB=CD=12cm,AD=BC=25cm,点E是AD上一点,且AE=9cm,连接BE,CE.判断∠BEC的锐角、钝角还是直角,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,∠C=90°,点0为△ABC的三条角平分线的交点,0D⊥BC,0E⊥AC,0F⊥AB,点D、E、F分别是垂足,且AB=5cm、BC=4cm,CA=3cm,则点0到三边AB、AC和BC的距离分别等于 ( )
如图,在△ABC中,∠C=90°,点0为△ABC的三条角平分线的交点,0D⊥BC,0E⊥AC,0F⊥AB,点D、E、F分别是垂足,且AB=5cm、BC=4cm,CA=3cm,则点0到三边AB、AC和BC的距离分别等于 ( )| A. | 1cm,1cm,1cm | B. | 1.5cm,1.5cm,1.5cm | ||
| C. | 2cm,2cm,2cm | D. | 2cm,1.5cm,1cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{x+y}{2}$是单项式 | |
| B. | 单项式可以看成是只有一项的多项式 | |
| C. | 单项式3(x2+1)的系数是3 | |
| D. | 多项式$\frac{3x-5}{4}$的常数项$\frac{5}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com