
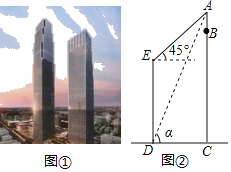
【题目】如图是长沙九龙仓国际金融中心,位于长沙市黄兴路与解放路交会处的东北角,投资160亿元人民币,总建筑面积达98万平方米,中心主楼BC高452m,是目前湖南省第一高楼,大楼顶部有一发射塔AB,已知和BC处于同一水平面上有一高楼DE,在楼DE底端D点测得A的仰角为α,tanα=![]() ,在顶端E点测得A的仰角为45°,AE=140
,在顶端E点测得A的仰角为45°,AE=140![]() m
m
(1)求两楼之间的距离CD;
(2)求发射塔AB的高度.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,有一个可以自由转动的转盘被平均分成3个扇形,分别标有1、2、3三个数字,小王和小李各转动一次转盘为一次游戏,当每次转盘停止后,指针所指扇形内的数为各自所得的数,一次游戏结束得到一组数(若指针指在分界线时重转).
(1)请你用树状图或列表的方法表示出每次游戏可能出现的所有结果;
(2)求每次游戏结束得到的一组数恰好是方程x2﹣3x+2=0的解的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,顶点为M的抛物线y=ax2+bx+3与x轴交于A(3,0),B(﹣1,0)两点,与y轴交于点C.
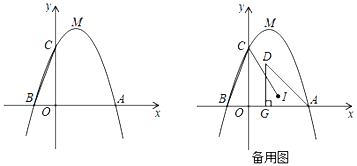
(1)求这条抛物线对应的函数表达式;
(2)问在y轴上是否存在一点P,使得△PAM为直角三角形?若存在,求出点P的坐标;若不存在,说明理由.
(3)若在第一象限的抛物线下方有一动点D,满足DA=OA,过D作DG⊥x轴于点G,设△ADG的内心为I,试求CI的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知,抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点,过点
两点,过点![]() 的直线
的直线![]() 与该抛物线交于点
与该抛物线交于点![]() ,点
,点![]() 是该抛物线上不与
是该抛物线上不与![]() 重合的动点,过点
重合的动点,过点![]() 作
作![]() 轴于
轴于![]() ,交直线
,交直线![]() 于点
于点![]() .
.
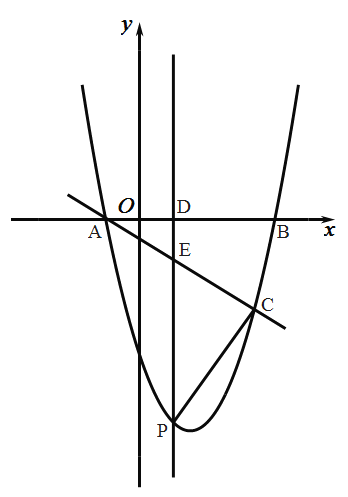
(1)求抛物线的解析式;
(2)若![]() ,当
,当![]() 时,求点
时,求点![]() 坐标;
坐标;
(3)当(2)中直线![]() 为
为![]() 时,是否存在实数
时,是否存在实数![]() ,使
,使![]() 与
与![]() 相似?若存在请求出
相似?若存在请求出![]() 的值;若不存在,请说明你的理由.
的值;若不存在,请说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有六个矩形水池环绕,矩形的内侧边所在直线恰好围成正六边形ABCDEF,正六边形的边长为4米.要从水源点P处向各水池铺设供水管道,这些管道的总长度最短是_____米.(结果保留根号)
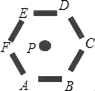
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,菱形
中,菱形![]() 的对角线
的对角线![]() 经过原点
经过原点![]() ,与
,与![]() 交于点
交于点![]() 轴于点
轴于点![]() ,点D的坐标
,点D的坐标![]() 为反比例函数
为反比例函数![]() 的图象恰好经过
的图象恰好经过![]() 两点.
两点.

(1)求![]() 的值及
的值及![]() 所在直线的表达式;
所在直线的表达式;
(2)求证:![]() .
.
(3)求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠D=∠B,补充下列条件之一,不一定能判定△ABC和△ADE相似的是( )
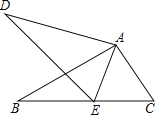
A.∠ACB=∠AEDB.∠CAE=∠BADC.∠BED=∠EACD.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com