
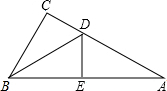
 如图所示,△ABC中,∠C=90°,DB平分∠ABC,DE垂直平分AB,试求∠ABC,若BC=8,AC=14,求△BCD的周长.
如图所示,△ABC中,∠C=90°,DB平分∠ABC,DE垂直平分AB,试求∠ABC,若BC=8,AC=14,求△BCD的周长. 科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
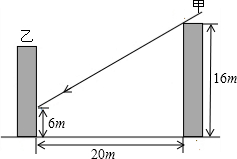 如图,某小区宿舍楼甲楼坐落在正南正北方向,高16m,现在在甲楼后盖座乙楼,冬天太阳最低时的正午时刻,若两楼相距20m,则甲楼的影子将落在乙楼6m,若甲楼的影子刚好不影响乙楼的采光,两楼距离应是多少m?
如图,某小区宿舍楼甲楼坐落在正南正北方向,高16m,现在在甲楼后盖座乙楼,冬天太阳最低时的正午时刻,若两楼相距20m,则甲楼的影子将落在乙楼6m,若甲楼的影子刚好不影响乙楼的采光,两楼距离应是多少m?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (3x3-5)(3x3+5)=9x6-25 | B. | (a+b+c+d)(a+b-c-d)=(a+b)2-(c+d)2 | ||
| C. | 50$\frac{1}{3}$×49$\frac{2}{3}$=502-($\frac{1}{3}$)2 | D. | 2(2a-b)2(4a+2b)2=(16a2-4b2)2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com