
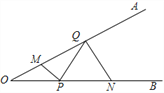
【题目】如图,∠AOB=30°,点M、N分别在边OA、OB上,且OM=1,ON=3,点P、Q分别在边OB、OA上,则MP+PQ+QN的最小值是____________
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=kx+b的图象分别交x轴、y轴于A、B两点,与反比例函数y= ![]() 交于C、D两点.已知点C坐标为(﹣4,﹣1),点D的横坐标为2.
交于C、D两点.已知点C坐标为(﹣4,﹣1),点D的横坐标为2.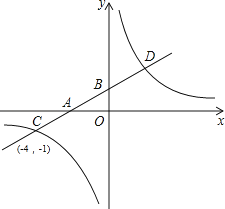
(1)求反比例函数与一次函数的解析式;
(2)若点P为坐标轴上一点,且S△ACP=2S△ABO , 请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知分式A=![]() .
.
(1) 化简这个分式;
(2) 当a>2时,把分式A化简结果的分子与分母同时加上3后得到分式B,问:分式B的值较原来分式A的值是变大了还是变小了?试说明理由.
(3) 若A的值是整数,且a也为整数,求出符合条件的所有a值的和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在△ABC中,∠BAC=90°,AB=AC,点D为直线BC上一动点(点D不与B、C重合).以AD为边作正方形ADEF,连接CF.
(1)如图1,当点D在线段BC上时,求证:①BD⊥CF.②CF=BC﹣CD.
(2)如图2,当点D在线段BC的延长线上时,其它条件不变,请直接写出CF、BC、CD三条线段之间的关系;
(3)如图3,当点D在线段BC的反向延长线上时,且点A、F分别在直线BC的两侧,其它条件不变:①请直接写出CF、BC、CD三条线段之间的关系.②若连接正方形对角线AE、DF,交点为O,连接OC,探究△AOC的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD中,∠D=100°,AC平分∠BCD,且∠ACB=40°,∠BAC=70°.

(1)AD与BC平行吗?试写出推理过程;
(2)求∠DAC和∠EAD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班级从甲乙两位同学中选派一人参加“秀美山河”知识竞赛,老师对他们的五次模拟成绩(单位:分)进行了整理,美工计算出甲成绩的平均数是80,甲乙成绩的方差分别是320,40,但绘制的统计图尚不完整.
甲乙两人模拟成绩统计表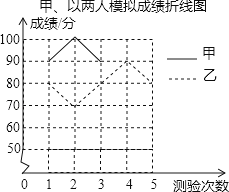
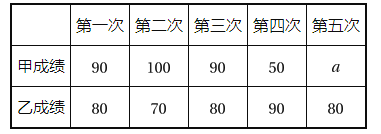
根据以上信息,请你解答下列问题:
(1)a=;
(2)请完成图中表示甲成绩变化情况的折线;
(3)求乙成绩的平均数;
(4)从平均数和方差的角度分析,谁将被选中.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD的面积是16,对角线AC、BD相交于点O,点M1、N1、P1分别为线段OD、DC、CO的中点,顺次连接M1N1、N1 P1、P1M1得到第一个△P1M1N1 , 面积为S1 , 分别取M1N1、N1P1、P1M1三边的中点P2、M2、N2 , 得到第二个△P2M2N2 , 面积记为S2 , 如此继续下去得到第n个△PnMnNn , 面积记为Sn , 则Sn﹣Sn﹣1= . (用含n的代数式表示,n≥2,n为整数)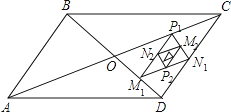
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com