
【题目】如图1, 在△ABC中,∠C=90°,AC=9cm,动点P从点A以1cm/s的速度沿AB向点B运动,运动到点B终止,同时动点Q从点B沿BA向点A匀速运动,运动到点A终止。设运动时间为x(s),P、Q之间的距离为y(cm),且y与x的函数图象如图2所示。
(1)动点Q的运动速度为 。
(2)点N所表示的实际意义是 。
(3)若△PQC的面积为18cm2,求运动的时间x

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】A校和B校分别库存有电脑12台和6台,现决定支援给C校10台和D校8台.已知从A校调运一台电脑到C校和D校的运费分别为40元和10元;从B校调运一台电脑到C校和D校的运费分别为30元和20元. 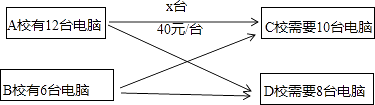
(1)设A校运往C校的电脑为x台,请仿照下图,求总运费W(元)关于x的函数关系式;
(2)求出总运费最低的调运方案,最低运费是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线F与x轴相交于A、B两点(点A在点B的左边),对称轴为直线x=1,顶点C在直线![]() 上,与y轴相交于点D(0,3)。
上,与y轴相交于点D(0,3)。
(1)求抛物线F的解析式;
(2)连结CD、BD,则线段BD与CD的数量关系和位置关系分别为 ;
(3)点P为直线CD上方抛物线F上的一个动点,PQ⊥CD,垂足为Q,若∠QPD=∠DBC,求点P的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
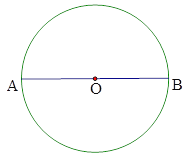
【题目】如图,AB是⊙O的直径,AB=2.
(1)尺规作图(保留作图痕迹,不写作法):作⊙O的内接正六边形ACDBEF。
(2)在(1)的条件下,直线PE与⊙O相切于点E,交AB延长线于点P,求PB、PE和![]() 所围成的图形面积。
所围成的图形面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小强同学对本校学生完成家庭作业的时间进行了随机抽样调查,并绘成如下不完整的三个统计图表.
组别 | 时间 (小时) | 频数 (人) | 频率 |
A | 0≤x≤0.5 | 20 | 0.2 |
B | 0.5<x≤1 | a | |
C | 1<x≤1.5 | ||
D | x>1.5 | 30 | 0.3 |
合计 | b | 1.0 | |
各组频数、频率统计表
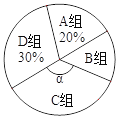
各组人数分布扇形统计图
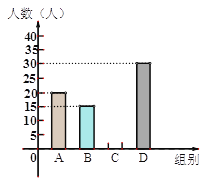
各组频数条形统计图
(1)a= ,b= ,∠α= ,并将条形统计图补充完整。
(2)若该校有学生3200人,估计完成家庭作业时间超过1小时的人数。
(3)根据以上信息,请您给校长提一条合理的建议。
查看答案和解析>>
科目:初中数学 来源: 题型:
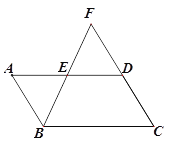
【题目】如图,□ABCD中,E为AD的中点,BE、CD相交于点F.
(1)求证:AB=DF
(2)若△DEF的面积为S1,△BCF的面积为S2,且S12-S2+4=0,求□ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某药品经过两次降价,每瓶零售价由168元降为108元,已知两次降价的百分率相同.设每次降价的百分率为x,根据题意列方程得( )
A.168(1+x)2=108B.168(1﹣x)2=108
C.168(1﹣2x)=108D.168y=x2(1﹣x2)=108
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com