
【题目】在Rt△ABC中,∠BAC=90°,AB=AC,D、E是斜边BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得△AFB,连接EF,下列结论:①△AED≌△AEF;②△ABC的面积等于四边形AFBD的面积;③BE+DC=DE;④BE2+DC2=DE2;⑤∠ADC=22.5°,其中正确的是( )

A. ①③④ B. ③④⑤ C. ①②④ D. ①②⑤
【答案】C
【解析】分析:①根据旋转的性质知∠CAD=∠BAF,AD=AF,因为∠BAC=90°,∠DAE=45°,所以∠CAD+∠BAE=45°,可得∠EAF=45°=∠DAE,由此即可证明△AEF≌△AED;
②根据旋转的性质,△ADC≌△ABF,进而得出△ABC的面积等于四边形AFBD的面积;
③根据①知道△ADE≌△AFE,得CD=BF,DE=EF;由此即可确定说法是否正确;
④据①BF=CD,EF=DE,∠FBE=90°,根据勾股定理判断.
⑤可以利用①②④正确,利用答案中没有更多正确答案,得出⑤错误.
详解:①根据旋转的性质知∠CAD=∠BAF,AD=AF.
∵∠BAC=90°,∠DAE=45°,∴∠CAD+∠BAE=45°,∴∠EAF=45°,∴△AEF≌△AED;
故①正确;
②∵根据旋转的性质,∴△ADC≌△ABF,∴△ABC的面积等于四边形AFBD的面积;
故此选项正确;
③根据①知道△ADE≌△AFE,得CD=BF,DE=EF,∴BE+DC=BE+BF>DE=EF,故③错误;
④∵AB=AC,△ADC旋转90°至△AFB,∴∠BAC=90°,∠ABC=∠ACB=45°,根据旋转的性质可得△ADC≌△ABF,∠ABF=∠ACD=45°,∴∠FBE=45°+45°=90°,∴BE2+BF2=EF2.
∵△ADC绕点A顺时针旋转90°后,得到△AFB,∴△AFB≌△ADC,∴BF=CD.
又∵EF=DE,∴BE2+CD2=DE2,故④正确.
⑤∵可以利用①②④正确,利用答案中没有更多正确答案,得出⑤错误.
故正确的有:①②④.
故选C.


 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:初中数学 来源: 题型:
【题目】某社区超市第一次用6000元购进甲、乙两种商品,其中乙商品的件数比甲商品件数的![]() 倍多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)
倍多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)
甲 | 乙 | |
进价(元/件) | 22 | 30 |
售价(元/件) | 29 | 40 |
(1)该超市购进甲、乙两种商品各多少件?
(2)该超市将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润?
(3)该超市第二次以第一次的进价又购进甲、乙两种商品,其中甲商品的件数不变,乙商品的件数是第一次的3倍;甲商品按原价销售,乙商品打折销售,第二次两种商品都销售完以后获得的总利润比第一次获得的总利润多180元,求第二次乙商品是按原价打几折销售?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系 xOy 中,点 A 是一次函数 y 3x 20 与 y x 12的交点,过点 A 分别作 x 、 y 轴的垂线段,垂足分别是 B 和C ,动点 P 和Q 以1个单位/秒的速度,分别从点C 、 B 出发,沿线段CA 、 BO 方向,向终点 A 、O 运动,设运动时间为t秒.

(1)证明:无论运动时间t 0 t 8取何值,四边形OPAQ 始终为平行四边形;
(2)当四边形OPAQ 为菱形时,请求出此时 PQ 的长度及直线 PQ 的函数解析式;
(3)当OP 满足 2![]() OP 5时,连接 PQ ,直线 PQ 与 y 轴交于点 M ,取线段 AC 的中点 N ,试确定 MNP 的面积 S 与运动的时间t 之间的函数关系式,并求出 S 的取值范围.
OP 5时,连接 PQ ,直线 PQ 与 y 轴交于点 M ,取线段 AC 的中点 N ,试确定 MNP 的面积 S 与运动的时间t 之间的函数关系式,并求出 S 的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正方形ABCO的顶点O在坐标远点,点B的坐标为(1,4),点A在第二象限,反比例函数![]() 的图像经过点A则K的值是()
的图像经过点A则K的值是()
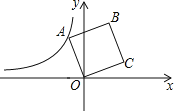
A.-2B.-4C.-8D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,以AC为直径作⊙O,交AB于D,过点O作OE∥AB,交BC于E.
(1)求证:ED为⊙O的切线;
(2)如果⊙O的半径为![]() ,ED=2,延长EO交⊙O于F,连接DF、AF,求△ADF的面积.
,ED=2,延长EO交⊙O于F,连接DF、AF,求△ADF的面积.

【答案】(1)证明见解析;(2)![]()
【解析】试题分析:(1)首先连接OD,由OE∥AB,根据平行线与等腰三角形的性质,易证得![]() ≌
≌![]() 即可得
即可得![]() ,则可证得
,则可证得![]() 为
为![]() 的切线;
的切线;
(2)连接CD,根据直径所对的圆周角是直角,即可得![]() 利用勾股定理即可求得
利用勾股定理即可求得![]() 的长,又由OE∥AB,证得
的长,又由OE∥AB,证得![]() 根据相似三角形的对应边成比例,即可求得
根据相似三角形的对应边成比例,即可求得![]() 的长,然后利用三角函数的知识,求得
的长,然后利用三角函数的知识,求得![]() 与
与![]() 的长,然后利用S△ADF=S梯形ABEF-S梯形DBEF求得答案.
的长,然后利用S△ADF=S梯形ABEF-S梯形DBEF求得答案.
试题解析:(1)证明:连接OD,

∵OE∥AB,
∴∠COE=∠CAD,∠EOD=∠ODA,
∵OA=OD,
∴∠OAD=∠ODA,
∴∠COE=∠DOE,
在△COE和△DOE中,
 ∴△COE≌△DOE(SAS),
∴△COE≌△DOE(SAS),
![]()
∴ED⊥OD,
∴ED是![]() 的切线;
的切线;
(2)连接CD,交OE于M,
在Rt△ODE中,
∵OD=32,DE=2,
![]()
∵OE∥AB,
∴△COE∽△CAB,
![]() ∴AB=5,
∴AB=5,
∵AC是直径,
![]()
![]()
![]()
![]()
∵EF∥AB,
![]()
![]()
![]()
∴S△ADF=S梯形ABEFS梯形DBEF
![]()
∴△ADF的面积为![]()

【题型】解答题
【结束】
25
【题目】【题目】已知,抛物线y=ax2+ax+b(a≠0)与直线y=2x+m有一个公共点M(1,0),且a<b.
(1)求b与a的关系式和抛物线的顶点D坐标(用a的代数式表示);
(2)直线与抛物线的另外一个交点记为N,求△DMN的面积与a的关系式;
(3)a=﹣1时,直线y=﹣2x与抛物线在第二象限交于点G,点G、H关于原点对称,现将线段GH沿y轴向上平移t个单位(t>0),若线段GH与抛物线有两个不同的公共点,试求t的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,![]() ,
,![]() ,过点D作
,过点D作![]() ,交
,交![]() 的平分线于点E,连接BE,延长DE交BC于F,
的平分线于点E,连接BE,延长DE交BC于F,![]() .
.
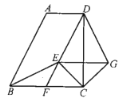
(1)求证:![]() .
.
(2)将![]() 绕点C顺时针旋转
绕点C顺时针旋转![]() 得到
得到![]() ,连接EG.求证:CD垂直平分EG.
,连接EG.求证:CD垂直平分EG.
(3)延长BE交CD于点P,求证:P是CD的中点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图四个几何体分别是三棱柱,四棱柱,五棱柱和六棱柱,三棱柱有5个面,9条棱,6个顶点,观察图形,填写下面的空.
(1)四棱柱有 个面, 条棱, 个顶点;
(2)六棱柱有 个面, 条棱, 个顶点;
(3)由此猜想n棱柱有 个面, 条棱, 个顶点.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将一个边长为![]() 的正方形纸片剪去两个小长方形,得到一个“6”的图案,如图2所示,再将剪下的两个小长方形拼成一个新的长方形,如图3所示,
的正方形纸片剪去两个小长方形,得到一个“6”的图案,如图2所示,再将剪下的两个小长方形拼成一个新的长方形,如图3所示,
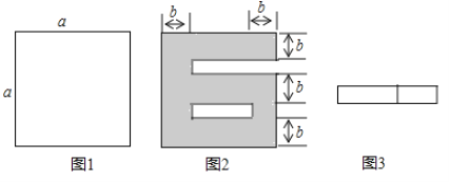
(1)这个新长方形的长和宽分别为________,_________;(用![]() 、
、![]() 的代数式表示)
的代数式表示)
(2)若![]() ,
,![]() ,求这个新长方形的周长.
,求这个新长方形的周长.
(3)在(2)的条件下,当![]() 时,求这个长方形的周长.
时,求这个长方形的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD,对角线的交点M(2,2).规定“把正方形ABCD先沿x轴翻折,再向左平移1个单位”为一次变换.如此这样,连续经过2014次变换后,正方形ABCD的对角线交点M的坐标变为( )
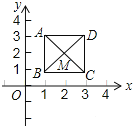
A. (﹣2012,2)B. (﹣2012,﹣2)C. (﹣2013,﹣2)D. (﹣2013,2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com