
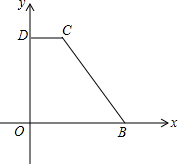
 如图,在平面直角坐标系中,点B为x轴正半轴上一点,点D为y轴正半轴上一点,CD∥OB,OB=14,CD=2,BC=13.若两动点E、F同时从O点出发,其中点E以每秒1个单位的速度沿折线O→D→C移动,点F以每秒2个单位的速度从点O向点B移动.
如图,在平面直角坐标系中,点B为x轴正半轴上一点,点D为y轴正半轴上一点,CD∥OB,OB=14,CD=2,BC=13.若两动点E、F同时从O点出发,其中点E以每秒1个单位的速度沿折线O→D→C移动,点F以每秒2个单位的速度从点O向点B移动.分析 (1)作CE⊥x轴于点G,则四边形ODCG是矩形,在直角△BCG中,利用勾股定理求得CG的长,则C和D的坐标即可求得;
(2)当0<t<5时,E在OD上,F在OB上,根据S=S梯形OBCD-S△CDE-S△OEF即可求解;5≤t≤7时,E在CD上,F在OB上,利用梯形面积公式即可求解;
(3)根据(2)的结果分两种情况,列方程即可求解.
解答 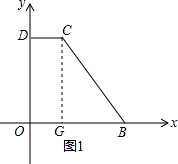 解:(1)作CE⊥x轴于点G,则四边形ODCG是矩形.
解:(1)作CE⊥x轴于点G,则四边形ODCG是矩形.
OG=CD,则BG=OB-OG=14-2=12M
在直角△BCE中,CG=$\sqrt{B{C}^{2}-B{G}^{2}}$=$\sqrt{1{3}^{2}-1{2}^{2}}$=5.
则C的坐标是(2,5),D的坐标是(0,5);
(2)当0<t<5时,E在OD上,F在OB上.
如图2.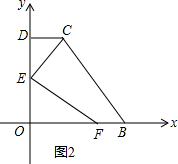 S梯形OBCD=$\frac{1}{2}$(CD+OB)•OD=$\frac{1}{2}$(2+14)×5=40;
S梯形OBCD=$\frac{1}{2}$(CD+OB)•OD=$\frac{1}{2}$(2+14)×5=40;
△CDE中,CD=2,DE=5-t.
则S△CDE=$\frac{1}{2}$CD•DE=$\frac{1}{2}$×2×(5-t)=5-t;
△OEF中,OE=t,OF=2t,
则S△OEF=$\frac{1}{2}$OE•OF=$\frac{1}{2}$×t•2t=t2.
则S=40-(5-t)-t2,
即S=-t2+t+35;
当5≤t≤7时,E在CD上,F在OB上,如图3. EC=7-t,BF=14-2t.
EC=7-t,BF=14-2t.
则S=$\frac{1}{2}$(EC+BF)•OD=$\frac{1}{2}$(7-t+14-2t)×5=$\frac{5}{2}$(21-3t)=-$\frac{15}{2}$t+$\frac{105}{2}$;
(3)当0<t<5时,-t2+t+35=$\frac{3}{8}$×40,
解得:t1=5(舍去),t2=-4.(舍去);
当5≤t≤7时,-$\frac{15}{2}$t+$\frac{105}{2}$=$\frac{3}{8}$×40,
解得:t=5.
则当t=5时,四边形CEFB的面积为梯形OBCD面积的$\frac{3}{8}$.
点评 本题考查了梯形的计算以及勾股定理,梯形的问题长通过作高线转化为直角三角形的问题,注意到分情况讨论是关键.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在平面直角坐标系中,正方形ABCD的顶点A落在y轴上,点C落在x轴上,随着顶点C由原点O向x轴正半轴方向运动,顶点A沿y轴负半轴方向运动到终点O,在运动过程中OD的长度变化情况是( )
如图,在平面直角坐标系中,正方形ABCD的顶点A落在y轴上,点C落在x轴上,随着顶点C由原点O向x轴正半轴方向运动,顶点A沿y轴负半轴方向运动到终点O,在运动过程中OD的长度变化情况是( )| A. | 一直增大 | B. | 一直减小 | C. | 先减小后增大 | D. | 先增大后减少 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
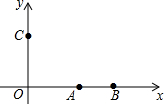 如图,已知点平面直角坐标系内三点A(3,0)、B(5,0)、C(0,4),⊙P经过点A、B、C,则点P的坐标为( )
如图,已知点平面直角坐标系内三点A(3,0)、B(5,0)、C(0,4),⊙P经过点A、B、C,则点P的坐标为( )| A. | (6,8) | B. | (4,5) | C. | (4,$\frac{31}{8}$) | D. | (4,$\frac{33}{8}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com