
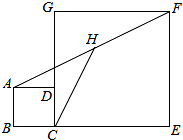
 如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH的长是
如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH的长是| 1 |
| 2 |
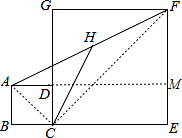 延长AD交EF于M,连接AC、CF,
延长AD交EF于M,连接AC、CF,| 1 |
| 2 |
| AM2+FM2 |
| 42+22 |
| 5 |
| 5 |
| 5 |
| 1 |
| 2 |


科目:初中数学 来源: 题型:
 P是等边△ABC的边AB上一点,连结PC,Q、D在PC、BC上,连结BQ、DQ、AD,且∠PQB=∠BQD=∠CQD,若BQ=3,QC=6,求AD的长为
P是等边△ABC的边AB上一点,连结PC,Q、D在PC、BC上,连结BQ、DQ、AD,且∠PQB=∠BQD=∠CQD,若BQ=3,QC=6,求AD的长为查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 将图中的正方形纸片沿虚线剪开,可得到4个全等的直角三角形和一个小的正方形,你会用所得的5个张纸片分别拼出一个轴对称图形和一个中心对称图形吗?请画出你的作品.
将图中的正方形纸片沿虚线剪开,可得到4个全等的直角三角形和一个小的正方形,你会用所得的5个张纸片分别拼出一个轴对称图形和一个中心对称图形吗?请画出你的作品.查看答案和解析>>
科目:初中数学 来源: 题型:
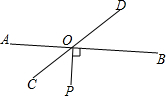 如图所示,草原上有两条交叉的河流AB,CD,有一个牧民在点P处放牧,且OP⊥AB于点O,理论上若他欲使羊群喝水的路程最短,他应作何选择?请你画出图形说明.
如图所示,草原上有两条交叉的河流AB,CD,有一个牧民在点P处放牧,且OP⊥AB于点O,理论上若他欲使羊群喝水的路程最短,他应作何选择?请你画出图形说明.查看答案和解析>>
科目:初中数学 来源: 题型:
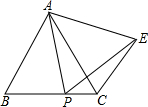 如图,△ABC是等边三角形,P为BC上一动点(不与B、C重合),以AP为边作等边△APE,连接CE.
如图,△ABC是等边三角形,P为BC上一动点(不与B、C重合),以AP为边作等边△APE,连接CE.查看答案和解析>>
科目:初中数学 来源: 题型:
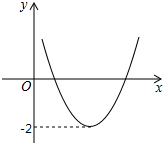 二次函数y=ax2+bx+c(a≠0)的图象如图所示,若|ax2+bx+c|=k(k≠0)有四个实数根,则k的取值范围是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,若|ax2+bx+c|=k(k≠0)有四个实数根,则k的取值范围是( )| A、k<2 | B、k>2 |
| C、0<k<2 | D、-2<k<2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com