
如图,已知△ABC是边长为6cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC匀速运动,其中点P运动的速度是1cm/s,点Q运动的速度是2cm/s,当点Q到达点C时,P、Q两点都停止运动,设运动时间为t(s),解答下列问题:
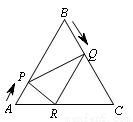
(1)当t=2时,判断△BPQ的形状,并说明理由;
(2)设△BPQ的面积为S(cm2),求S与t的函数关系式;
(3)作QR//BA交AC于点R,连结PR,当t为何值时,△APR∽△PRQ?
(1)△BPQ是等边三角形;(2)S=-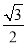 t2+3
t2+3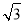 t;(3)当t=
t;(3)当t=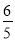 时,△APR∽△PRQ.
时,△APR∽△PRQ.
【解析】
试题分析:(1)当t=2时,可分别计算出BP、BQ的长,再对△BPQ的形状进行判断;
(2)∠B为60°特殊角,过Q作QE⊥AB,垂足为E,则BQ、BP、高EQ的长可用t表示,S与t的函数关系式也可求;
(3)由题目线段的长度可证得△CRQ为等边三角形,进而得出四边形EPRQ是矩形,由△APR∽△PRQ,可得出∠QPR=60°,利用60°的特殊角列出一方程即可求得t的值.
试题解析:(1)△BPQ是等边三角形
当t=2时
AP=2×1=2,BQ=2×2=4
∴BP=AB-AP=6-2=4
∴BQ=BP
又∵∠B=60°
∴△BPQ是等边三角形;
(2)过Q作QE⊥AB,垂足为E
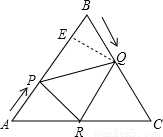
由QB=2t,得QE=2t•sin60°=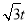
由AP=t,得PB=6-t
∴S△BPQ=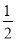 ×BP×QE=
×BP×QE=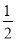 (6-t)×
(6-t)×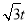 =-
=-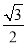 t2+3
t2+3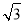 t
t
∴S=-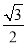 t2+3
t2+3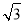 t
t
(3)∵QR∥BA
∴∠QRC=∠A=60°,∠RQC=∠B=60°
∴△QRC是等边三角形
∴QR=RC=QC=6-2t
∵BE=BQ•cos60°=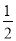 ×2t=t
×2t=t
∴EP=AB-AP-BE=6-t-t=6-2t
∴EP∥QR,EP=QR
∴四边形EPRQ是平行四边形
∴PR=EQ=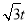
又∵∠PEQ=90°,
∴∠APR=∠PRQ=90°
∵△APR∽△PRQ,
∴∠QPR=∠A=60°
∴tan60°=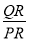
即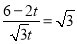
解得t=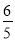
∴当t=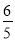 时,△APR∽△PRQ.
时,△APR∽△PRQ.
考点:1.相似三角形的性质;2.等边三角形的性质;3.平行四边形的性质;4.解直角三角形.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:初中数学 来源:2014-2015学年黑龙江省鸡西市八年级上学期期中考试数学试卷(解析版) 题型:选择题
如图,AB∥DE,∠B+∠C+∠D=( )
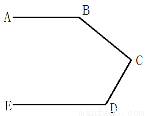
A、180° B、360° C、540° D、270°
查看答案和解析>>
科目:初中数学 来源:2014-2015学年四川省广安市九年级上期末考试模拟考试数学试卷(解析版) 题型:选择题
若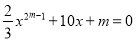 是关于
是关于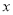 的一元二次方程,则m的值应为( )
的一元二次方程,则m的值应为( )
A.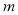 =2 B.
=2 B.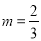 C.
C.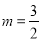 D.无法确定
D.无法确定
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省九年级上学期期末模拟考试数学试卷(解析版) 题型:填空题
如图所示,在宽为25m,长为36m的矩形耕地上,修筑同样宽的三条道路,(互相垂直),把耕地分成大小不等的六块试验田,要使试验田的面积为 590m2 ,道路应为多宽?若设道路的宽为x米,根据题意可列方程
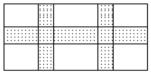
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省九年级上学期期末模拟考试数学试卷(解析版) 题型:选择题
依次连接菱形各边中点所成的四边形是( ).
A.平行四边形 B.矩形 C.菱形 D.正方形
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省启东市滨海实验校共同体九年级上学期第二次质检数学试卷(解析版) 题型:解答题
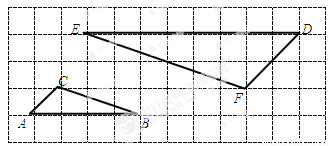
网格图中每个方格都是边长为1的正方形.若A,B,C,D,E,F都是格点,试说明△ABC∽△DEF.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年重庆市八年级上学期期末模拟数学试卷(解析版) 题型:解答题
已知:如图所示,
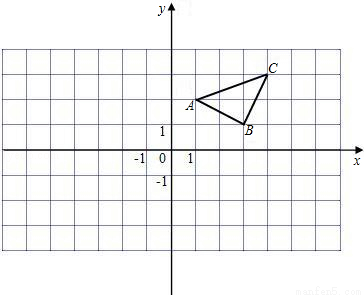
(1)作出△ABC关于y轴对称的△A′B′C′,并写出△A′B′C′三个顶点的坐标.
(2)在x轴上画出点P,使PA+PC最小.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省八年级上学期期中检测数学试卷(解析版) 题型:选择题
如图,在△ABC中,AB=AC,∠ABC、∠ACB的平分线相交于点D,过点D作直线EF∥BC,交AB于E,交AC于F,图中等腰三角形的个数共有( )

A.3个 B.4个 C.5个 D.6个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com