
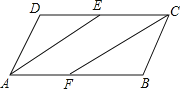
【题目】在ABCD中,AE平分∠DAB交CD于E点、CF平分∠DCB交AB于点F.
(1)求证:四边形AECF是平行四边形;
(2)若BG平分∠ABC交CD于G点,且AD=2EG=2,求四边形ABCD的周长.
【答案】(1)详见解析;(2)14或10.
【解析】
(1)由平行四边形的性质和角平分线的性质可得∠DEA=∠DCF,可证AE∥CF,即可得结论;
(2)分两种情况讨论,由角平分线的性质和平行四边形性质可求CD的长度,即可求四边形ABCD的周长.
证明:(1)∵四边形ABCD是平行四边形
∴AB∥CD,∠DAB=∠DCB
∵AE平分∠DAB交CD于E点、CF平分∠DCB交AB于点F.
∴∠DAE=∠EAB=![]() ∠DAB,∠DCF=∠BCF=
∠DAB,∠DCF=∠BCF=![]() ∠DCB,
∠DCB,
∴∠EAB=∠DCF
∵AB∥CD
∴∠DEA=∠EAB
∴∠DEA=∠DCF
∴AE∥CF,且AB∥CD
∴四边形AECF是平行四边形;
(2)如图,当点G在点E右侧,
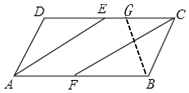
∵四边形ABCD是平行四边形
∴AB∥CD,AD=BC=2
∵AE平分∠DAB,
∴∠DAE=∠EAB
∵AB∥CD
∴∠DEA=∠EAB
∴∠AED=∠DAE
∴AD=DE=2,
同理可得:BC=GC=2
∵AD=2EG=2
∴EG=1
∴CD=DE+EG+GC=5
∴四边形ABCD的周长=2(AD+CD)=14
如图,若点G在点E左侧,

同理可得:DE=GC=2,GE=1
∴CD=DE+EC﹣GE=3
∴四边形ABCD的周长=2(AD+CD)=10
综上所述,四边形ABCD的周长为14或10.


 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源: 题型:
【题目】如图,已知:∠MON=30o,点A1、A2、A3 在射线ON上,点B1、B2、B3…..在射线OM上,△A1B1A2. △A2B2A3、△A3B3A4……均为等边三角形,若OA1=l,则△A6B6A7 的边长为【 】

A.6 B.12 C.32 D.64
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,点O是边BC的中点,连接DO并延长,交AB延长线于点E,连接BD,EC.
(1)求证:四边形BECD是平行四边形;
(2)若∠A=50°,则当∠BOD= ______ °时,四边形BECD是矩形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,B,C三点在⊙O上,直径BD平分∠ABC,过点D作DE∥AB交弦BC于点E,在BC的延长线上取一点F,使得EF![]() DE.
DE.
(1)求证:DF是⊙O的切线;
(2)连接AF交DE于点M,若 AD![]() 4,DE
4,DE![]() 5,求DM的长.
5,求DM的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AB=3,点E,F分别在CD,AD上,CE=DF,BE,CF相交于点G.若图中阴影部分的面积与正方形ABCD的面积之比为2:3,则△BCG的周长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y1=﹣2x2+2,直线y2=2x+2,当x任取一值时,x对应的函数值分别为y1、y2.若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M=y1=y2.例如:当x=1时,y1=0,y2=4,y1<y2,此时M=0.下列判断:
①当x>0时,y1>y2; ②当x<0时,x值越大,M值越小;
③使得M大于2的x值不存在; ④使得M=1的x值是![]() 或
或![]() .
.
其中正确的是( )

A.①② B.①④ C.②③ D.③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() (a ≠ 0)满足条件:(1)
(a ≠ 0)满足条件:(1)![]() ;(2)
;(2)![]() ;
;
(3)与x轴有两个交点,且两交点间的距离小于2.以下有四个结论:①![]() ;
;
②![]() ;③
;③![]() ;④
;④![]() ,其中所有正确结论的序号是
,其中所有正确结论的序号是
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于A(-1,0),B(3,0)两点,与
轴交于A(-1,0),B(3,0)两点,与![]() 轴交于点C,顶点为D,下列结论正确的是( )
轴交于点C,顶点为D,下列结论正确的是( )

A. abc<0 B. 3a+c=0 C. 4a-2b+c<0 D. 方程ax2+bx+c=-2(a≠0)有两个不相等的实数根
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:一个自然数,右边的数字总比左边的数字小,我们称它为“下滑数”(如:32,641,8531等).现从两位数中任取一个,恰好是“下滑数”的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com