
科目:初中数学 来源: 题型:解答题
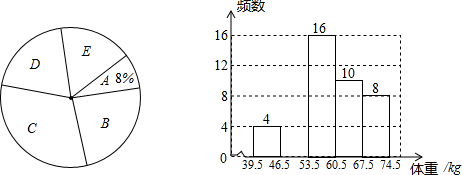
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1-$\sqrt{2}$ | B. | 2-$\sqrt{2}$ | C. | 1+$\sqrt{2}$或1-$\sqrt{2}$ | D. | 1+$\sqrt{2}$或-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
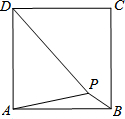 在正方形ABCD内有一点P,且PA=2$\sqrt{2}$,PB=1,PD=$\sqrt{17}$,则正方形ABCD的边长为$\sqrt{13}$.
在正方形ABCD内有一点P,且PA=2$\sqrt{2}$,PB=1,PD=$\sqrt{17}$,则正方形ABCD的边长为$\sqrt{13}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
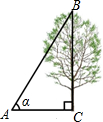 如图,在地面上的点A处测得树顶B的仰角为α度,AC=7米,则树高BC为( )米.
如图,在地面上的点A处测得树顶B的仰角为α度,AC=7米,则树高BC为( )米.| A. | 7tanα | B. | $\frac{7}{tanα}$ | C. | 7sinα | D. | 7cosα |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图是一张边长为8的正方形纸片,在正方形纸片上剪下一个腰长为5的等腰三角形(要求:等腰三角形的一个顶点与正方形的一个顶点重合,其余两个顶点在正方形的边上),则剪下的等腰三角形的底边长是( )
如图是一张边长为8的正方形纸片,在正方形纸片上剪下一个腰长为5的等腰三角形(要求:等腰三角形的一个顶点与正方形的一个顶点重合,其余两个顶点在正方形的边上),则剪下的等腰三角形的底边长是( )| A. | 4$\sqrt{3}$ | B. | 5$\sqrt{2}$ | C. | 4$\sqrt{3}$或5$\sqrt{2}$ | D. | 4$\sqrt{5}$或5$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
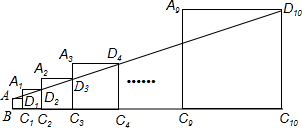 已知正方形ABC1D1的边长为1,延长C1D1到A1,以A1C1为边向右作正方形A1C1C2D2,延长C2D2到A2,以A2C2为边向右作正方形A2C2C3D3(如图所示),以此类推….若A1C1=2,且点A,D2,D3,…,D10都在同一直线上,则正方形A9C9C10D10的边长是$\frac{{3}^{8}}{{2}^{7}}$.
已知正方形ABC1D1的边长为1,延长C1D1到A1,以A1C1为边向右作正方形A1C1C2D2,延长C2D2到A2,以A2C2为边向右作正方形A2C2C3D3(如图所示),以此类推….若A1C1=2,且点A,D2,D3,…,D10都在同一直线上,则正方形A9C9C10D10的边长是$\frac{{3}^{8}}{{2}^{7}}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
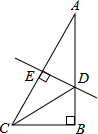 如图,在Rt△ABC中,∠B=90°,∠A=30°,DE垂直平分斜边AC,交AB于D,E是垂足,连接CD.若BD=1,则AC的长是( )
如图,在Rt△ABC中,∠B=90°,∠A=30°,DE垂直平分斜边AC,交AB于D,E是垂足,连接CD.若BD=1,则AC的长是( )| A. | 2$\sqrt{3}$ | B. | 2 | C. | 4$\sqrt{3}$ | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com