
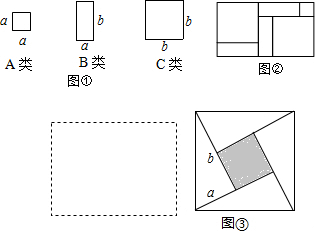
���� ��1������ͼ�Σ����ͼ��������ʽ�ó����ɣ�
��2������ͼ�ε�������ɵõ����ۣ�
��3���ٸ��ݵ�ʽ���ɵó���3�ţ��ڸ�����ȫƽ����ʽ�жϼ��ɣ�
���  �⣺��1����ͼ��
�⣺��1����ͼ��
��a+b����a+b��=a2+2ab+b2��
�ʴ�Ϊ��a2+2ab+b2��
��2�������ε����Ϊa2+3ab+2b2��
�ʴ�Ϊ��a2+3ab+2b2��
��3���١�3a2+4ab+b2=��3a+b����a+b����
����ҪB�Ƭ4�ţ�
�ʴ�Ϊ��4��
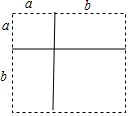
��3���⣺����ͼ�۵ã�4��$\frac{1}{2}$ab+n2=m2��
��ab=$\frac{{m}^{2}-{n}^{2}}{2}$��
�ߣ�b-a��2=n2��4��$\frac{1}{2}$ab+n2=2ab+��b-a��2=m2��
��a2+b2=m2��
�ࣨ1������4����ȷ��
�ʴ�Ϊ����1������4����
���� ���⿼���˷ֽ���ʽ�������ε��������ȫƽ����ʽ��Ӧ�ã���Ҫ����ѧ���Ĺ۲�ͼ�ε������ͻ���������


 ���㼤�������100�ִ��Ծ�ϵ�д�
���㼤�������100�ִ��Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
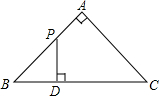 ��ͼ����ABC�ǵ���ֱ�������Σ���A=90�㣬BC=4����P�ǡ�ABC�ı���һ���㣬��B��A��C��·���ƶ�������P��PD��BC�ڵ�D����BD=x����BDP�����Ϊy����y��x������ϵ��ͼ������ǣ�������
��ͼ����ABC�ǵ���ֱ�������Σ���A=90�㣬BC=4����P�ǡ�ABC�ı���һ���㣬��B��A��C��·���ƶ�������P��PD��BC�ڵ�D����BD=x����BDP�����Ϊy����y��x������ϵ��ͼ������ǣ�������| A�� | 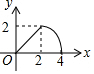 | B�� | 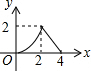 | C�� | 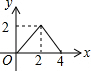 | D�� | 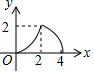 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
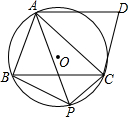 ��֪����ͼ����ƽ���ı���ABCD�У���O�Ǿ���A��B��C�����Բ��CD���O�����ڵ�C����P��$\widehat{BC}$�ϵ�һ�����㣨��P����B��C���غϣ�������PA��PB��PC��
��֪����ͼ����ƽ���ı���ABCD�У���O�Ǿ���A��B��C�����Բ��CD���O�����ڵ�C����P��$\widehat{BC}$�ϵ�һ�����㣨��P����B��C���غϣ�������PA��PB��PC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0.64m | B�� | 0.8m | C�� | 8m | D�� | 10m |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com