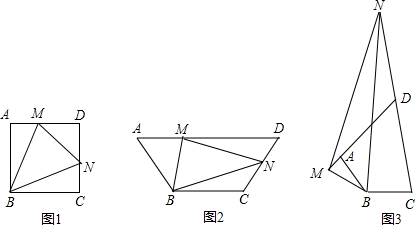
(1)解:

延长DC到Q,使CQ=AF,连接BQ,
∵正方形ABCD,
∴AB=BC,∠A=∠DCB=∠BCQ=∠ABC=90°,
在△ABF和△CBQ中

,
∴△ABF≌△CBQ,
∴BF=BQ,∠ABF=∠CBQ,
∵∠ABC=90°,∠EBF=45°,
∴∠ABF+∠EBC=45°,
∴∠EBC+∠CBQ=45°=∠EBQ=∠EBF,
在△EBF和△EBQ中
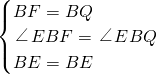
,
∴△EBF≌△EBQ,
∴EF=EQ=10,
∴△BEF的面积等于△EBQ的面积,即

EQ×BC=

×10×12=60.
答:△BEF的面积是60.
(2)解:设CE=x,则DE=12-x,DF=12-AF=12-CQ=12-(10-x)=2+x,
在△DEF中,由勾股定理得:DE
2+DF
2=EF
2,
即(12-x)
2+(2+x)
2=10
2,
解得:x
1=4,x
2=18>10(舍去),
∴CE=4.
分析:(1)延长DC到Q,使CQ=AF,连接BQ,根据正方形性质推出AB=BC,∠A=∠DCB=∠BCQ=∠ABC=90°,根据SAS证△ABF≌△CBQ,推出BF=BQ,∠ABF=∠CBQ,求出∠EBQ=∠EBF,根据△EBF≌△EBQ,推出EF=EQ=10,根据△BEF的面积等于△EBQ的面积,代入求出即可;
(2)设CE=x,则得出E=12-x,DF═2+x,在△DEF中根据勾股定理得出DE
2+DF
2=EF
2,代入得出方程,求出方程的解即可.
点评:本题考查了正方形性质,勾股定理,全等三角形的性质和判定,三角形的面积等知识点的运用,解(1)小题的关键是正确作辅助线,并证出△EBF≌△EBQ,解(2)小题的关键是在(1)的基础式得出一个关于x的方程,用的数学思想是方程思想和转化思想,题目比较好,具有一定的代表性.

 在正方形ABCD中,AB=12,E在边CD上,∠EBF=45°,EF=10.
在正方形ABCD中,AB=12,E在边CD上,∠EBF=45°,EF=10.
 ,
,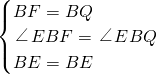 ,
, EQ×BC=
EQ×BC= ×10×12=60.
×10×12=60.

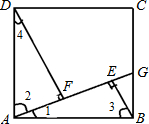 18、在正方形ABCD中,点G是BC上任意一点,连接AG,过B,D两点分别作BE⊥AG,DF⊥AG,垂足分别为E,F两点,求证:△ADF≌△BAE.
18、在正方形ABCD中,点G是BC上任意一点,连接AG,过B,D两点分别作BE⊥AG,DF⊥AG,垂足分别为E,F两点,求证:△ADF≌△BAE.