
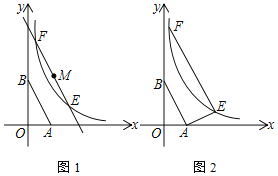
ЁОЬтФПЁПШчЭМ1ЃЌAЃЈ1ЃЌ0ЃЉЁЂBЃЈ0ЃЌ2ЃЉЃЌЫЋЧњЯпyЃН![]() ЃЈxЃО0ЃЉ
ЃЈxЃО0ЃЉ
ЃЈ1ЃЉШєНЋЯпЖЮABШЦAЕуЫГЪБеыа§зЊ90ЁуКѓBЕФЖдгІЕуЧЁКУТфдкЫЋЧњЯпyЃН![]() ЃЈxЃО0ЃЉЩЯ
ЃЈxЃО0ЃЉЩЯ
ЂйдђkЕФжЕЮЊЁЁ ЃЛ
ЂкНЋжБЯпABЦНвЦгыЫЋЧњЯпyЃН![]() ЃЈxЃО0ЃЉНЛгкEЁЂFЃЌEFЕФжаЕуЮЊMЃЈaЃЌbЃЉЃЌЧѓ
ЃЈxЃО0ЃЉНЛгкEЁЂFЃЌEFЕФжаЕуЮЊMЃЈaЃЌbЃЉЃЌЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉНЋжБЯпABЦНвЦгыЫЋЧњЯпyЃН![]() ЃЈxЃО0ЃЉНЛгкEЁЂFЃЌСЌНгAEЃЎШєABЁЭAEЃЌЧвEFЃН2ABЃЌШчЭМ2ЃЌжБНгаДГіkЕФжЕЁЁ ЃЎ
ЃЈxЃО0ЃЉНЛгкEЁЂFЃЌСЌНгAEЃЎШєABЁЭAEЃЌЧвEFЃН2ABЃЌШчЭМ2ЃЌжБНгаДГіkЕФжЕЁЁ ЃЎ
ЁОД№АИЁПЃЈ1ЃЉЂйkЃН3ЃЛЂк2ЃЛЃЈ2ЃЉkЃН![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЯШЧѓГіAЁЂBЕуЕФзјБъЃЌдйЧѓГіа§зЊКѓBЕуЕФзјБъЃЌНјЖјгЩД§ЖЈЯЕЪ§ЗЈЧѓГіkБуПЩЃЛ
ЃЈ2ЃЉЩшГіEFЕФНтЮіЪНЃЌдйЧѓГіЕуEЁЂFЕФзјБъЃЌгЩжаЕузјБъЙЋЪНЧѓЕУMЕуЕФзјБъЃЌНјЖјЧѓ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉгЩЁїABOЁзЁїEHAЕУЃК![]() ЃЌЩшEH=mЃЌдђAH=2mЃЌЧѓГіEFЕФБэДяЪНВЂгыЗДБШР§КЏЪ§БэДяЪНСЊСЂЧѓГіЕуFзјБъЃЌМДПЩЧѓНт
ЃЌЩшEH=mЃЌдђAH=2mЃЌЧѓГіEFЕФБэДяЪНВЂгыЗДБШР§КЏЪ§БэДяЪНСЊСЂЧѓГіЕуFзјБъЃЌМДПЩЧѓНт
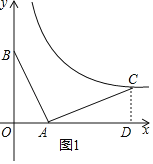
ЃЈ1ЃЉЂйЩша§зЊКѓЕуBЕФЖдгІЕуЮЊЕуCЃЌЙ§ЕуCзїCDЁЭxжсгкЕуDЃЌШчЭМЫљЪО
ЁпЁЯBACЃН90ЁуЃЌ
ЁрЁЯBAO+ЁЯCADЃН90ЁуЃЌ
ЁпЁЯBAO+ЁЯABOЃН90ЁуЃЌ
ЁрЁЯABOЃНЁЯCADЃЌ
дкЁїOABКЭЁїDCAжаЃЌ
 ЃЌ
ЃЌ
ЁрЁїOABЁеЁїDCAЃЈAASЃЉЃЌ
ЁрCDЃНOAЃН1ЃЌ
ADЃНOBЃН2ЃЌ
ЁрODЃНOA+ADЃН3ЃЌ
ЁрCЃЈ3ЃЌ1ЃЉЃЌ
АбCЃЈ3ЃЌ1ЃЉДњШыyЃН![]() жаЃЌЕУkЃН3ЃЌ
жаЃЌЕУkЃН3ЃЌ
ЙЪД№АИЮЊ3ЃЛ
ЂкжБЯпABБэДяЪНжаЕФkжЕЮЊЉ2ЃЌABЁЮEFЃЌдђжБЯпEFБэДяЪНжаЕФkжЕЮЊЉ2ЃЌ
ЩшЕуEЃЈmЃЌnЃЉЃЌmnЃН3ЃЌ
жБЯпEFЕФБэДяЪНЮЊЃКyЃНЉ2x+tЃЌ
НЋЕуEзјБъДњШыЩЯЪНВЂНтЕУЃЌжБЯпEFЕФБэДяЪНЮЊyЃНЉ2x+2m+nЃЌ
НЋжБЯпEFБэДяЪНгыЗДБШР§КЏЪ§БэДяЪНСЊСЂВЂећРэЕУЃК
2x2ЉЃЈ2m+nЃЉx+3ЃН0ЃЌ
x1+x2ЃН![]() ЃЌx1x2ЃН
ЃЌx1x2ЃН![]() ЃЌ
ЃЌ
дђЕуFЃЈ![]() nЃЌ
nЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
дђaЃН![]() ЃЈ
ЃЈ![]() ЃЉЃЌbЃН
ЃЉЃЌbЃН![]() ЃЈn+
ЃЈn+![]() ЃЉЃЌ
ЃЉЃЌ
![]() ЃН2ЃЛ
ЃН2ЃЛ
ЃЈ2ЃЉЙЪЕуEзїEHЁЭxжсНЛгкЕуHЃЌ

гЩЃЈ1ЃЉжЊЃКЁїABOЁзЁїEHAЃЌ
Ёр![]() ЃЌЩшEHЃНmЃЌдђAHЃН2mЃЌ
ЃЌЩшEHЃНmЃЌдђAHЃН2mЃЌ
дђЕуEЃЈ2m+1ЃЌmЃЉЃЌЧвkЃНmЃЈ2m+1ЃЉЃН2m2+mЃЌ
жБЯпABБэДяЪНжаЕФkжЕЮЊЉ2ЃЌABЁЮEFЃЌдђжБЯпEFБэДяЪНжаЕФkжЕЮЊЉ2ЃЌ
ЩшжБЯпEFЕФБэДяЪНЮЊЃКyЃНЉ2x+bЃЌНЋЕуEзјБъДњШыВЂЧѓНтЕУЃКbЃН5m+2ЃЌ
ЙЪжБЯпEFЕФБэДяЪНЮЊЃКyЃНЉ2x+5m+2ЃЌ
НЋЩЯЪНгыЗДБШР§КЏЪ§БэДяЪНСЊСЂВЂећРэЕУЃК2x2ЉЃЈ5m+2ЃЉx+3ЃН0ЃЌ
гУЮЄДяЖЈРэНтЕУЃКxF+xEЃН![]() ЃЌдђxFЃН
ЃЌдђxFЃН![]() ЃЌ
ЃЌ
дђЕуFЃЈ![]() mЃЌ4m+2ЃЉЃЌ
mЃЌ4m+2ЃЉЃЌ
дђEFЃН![]() ЃН2ABЃН2ЁС
ЃН2ABЃН2ЁС![]() ЃЌ
ЃЌ
ећРэЕУЃК3m2+4mЉ4ЃН0ЃЌ
НтЕУЃКmЃН![]() ЛђЉ2ЃЈЩсШЅИКжЕЃЉЃЌ
ЛђЉ2ЃЈЩсШЅИКжЕЃЉЃЌ
kЃНmЃЈ2m+1ЃЉЃН2m2+mЃН![]() ЃЎ
ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвЛДЮКЏЪ§yЃНk1xЃЋbЕФЭМЯѓгыЗДБШР§КЏЪ§yЃН![]() (xЃМ0)ЕФЭМЯѓЯрНЛгкЕуA(Ѓ1ЃЌ2)ЁЂЕуB(Ѓ4ЃЌn)ЃЎ
(xЃМ0)ЕФЭМЯѓЯрНЛгкЕуA(Ѓ1ЃЌ2)ЁЂЕуB(Ѓ4ЃЌn)ЃЎ
(1)ЧѓДЫвЛДЮКЏЪ§КЭЗДБШР§КЏЪ§ЕФБэДяЪНЃЛ
(2)ЧѓЁїAOBЕФУцЛ§ЃЛ
(3)дкxжсЩЯДцдквЛЕуPЃЌЪЙЁїPABЕФжмГЄзюаЁЃЌЧѓЕуPЕФзјБъЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЖўДЮКЏЪ§ЕФЭМЯѓОЙ§![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() Ш§ЕуЃЎ
Ш§ЕуЃЎ
ЃЈ1ЃЉЧѓИУЖўДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЕу![]() ЪЧЯпЖЮ
ЪЧЯпЖЮ![]() ЩЯЕФЖЏЕуЃЈЕу
ЩЯЕФЖЏЕуЃЈЕу![]() гыЯпЖЮ
гыЯпЖЮ![]() ЕФЖЫЕуВЛжиКЯЃЉЃЌШє
ЕФЖЫЕуВЛжиКЯЃЉЃЌШє![]() гы
гы![]() ЯрЫЦЃЌЧѓЕу
ЯрЫЦЃЌЧѓЕу![]() ЕФзјБъЃЎ
ЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
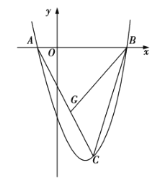
ЁОЬтФПЁПвбжЊЁїOABдкЦНУцжБНЧзјБъЯЕжаЕФЮЛжУШчЭМЫљЪОЃЌНЋЁїABOШЦдЕуOФцЪБеыа§зЊ90ЁуЕУЕНЁїOA1B1ЃЎ

ЃЈ1ЃЉЛГіЁїOA1B1ЃЌВЂаДГіЕуA1ЁЂB1ЕФзјБъЃЛ
ЃЈ2ЃЉЧѓЁїABOШЦдЕуOФцЪБеыа§зЊ90ЁуЩЈЙ§ЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЁїABCжаЃЌЁЯACB=90ЁуЃЌAC=BCЃЌЕуPдкБпABЩЯЃЌЕуDЁЂQЗжБ№ЮЊБпBCЩЯЕФЕуЃЌЯпЖЮADЕФбгГЄЯпгыЯпЖЮPQЕФбгГЄЯпНЛгкЕуFЃЌСЌНгCPНЛAFгкЕуEЃЌШєЁЯBPF=ЁЯAPCЃЌFD=FQЃЎ
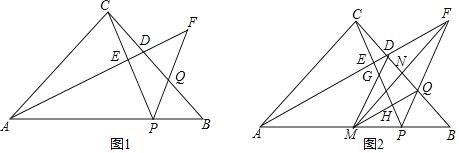
ЃЈ1ЃЉШчЭМ1ЃЌЧѓжЄЃКAFЁЭCPЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌзїЁЯAFPЕФЦНЗжЯпFMНЛABгкЕуMЃЌНЛBCгкЕуNЃЌШєFN=MNЃЌЧѓжЄЃК![]() ЃЛ
ЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌСЌНгDMЁЂMQЃЌЗжБ№НЛPCгкЕуGЁЂHЃЌЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкбЇЯАЁАЖўдЊвЛДЮЗНГЬзщЕФНтЁБЪБЃЌЪ§бЇеХРЯЪІЩшМЦСЫвЛИіЪ§бЇЛюЖЏЃЌгаAЁЂBСНзщПЈЦЌЃЌУПзщИїШ§еХЃЌAзщПЈЦЌЩЯЗжБ№аДга0,1,2ЃЛBзщПЈЦЌЩЯЗжБ№аДга-3ЃЌ-1,1ЁЃУПеХПЈЦЌГ§е§УцаДгаВЛЭЌЪ§зжЭтЃЌЦфгрОљЯрЭЌЁЃМзДгAзщЫцЛњГщШЁвЛеХМЧЮЊxЃЌввДгBзщЫцЛњГщШЁвЛеХМЧЮЊyЁЃ
(1)ШєМзГщГіЕФЪ§зжЪЧ2ЃЌввГщГіЕФЪ§зжЪЧ-1ЃЌЫќУЧЧЁКУЪЧЗНГЬax-y=5ЕФНтЃЌЧѓaЕФжЕЃЛ
(2)ЧѓМзЁЂввЫцЛњГщШЁвЛДЮЕФЪ§ЧЁКУЪЧЗНГЬax-y=3ЕФНтЕУИХТЪЃЈЧыгУЪїзДЭМЛђСаБэЗЈЧѓНт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЁїABCдкЦНУцжБНЧзјБъЯЕжаЕФЮЛжУШчЭМЫљЪОЃЎ

ЃЈ1ЃЉЛГіЁїABCШЦЕуCАДЫГЪБеыЗНЯђа§зЊ90ЁуЕФЁїAЁфBЁфCЃЌВЂжБНгаДГіЕуAдка§зЊЙ§ГЬжаЫљОЙ§ЕФТЗОЖГЄЃЈНсЙћБЃСє![]() ЃЉЃЛ
ЃЉЃЛ
ЃЈ2ЃЉдкЃЈ1ЃЉЕФЬѕМўЯТЃЌРћгУГпЙцзїЭМЛГіЁїAЁфBЁфCЕФЭтНгдВЁбPЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМзЁЂввСНШЫНјааУўХЦгЮЯЗЯжгаШ§еХГ§Ъ§зжЭтЖМЯрЭЌЕФХЦЃЌе§УцЗжБ№БъгаЪ§зж2ЃЌ5ЃЌ6ЃЎНЋШ§еХХЦБГУцГЏЩЯЃЌЯДдШКѓЗХдкзРзгЩЯЃЎ
ЃЈ1ЃЉМзДгжаЫцЛњГщШЁвЛеХХЦЃЌМЧТМЪ§зжКѓЗХЛиЯДдШЃЌввдйЫцЛњГщШЁвЛеХЧыгУСаБэЗЈЛђЛЪїзДЭМЕФЗНЗЈЃЌЧѓСНШЫГщШЁЯрЭЌЪ§зжЕФИХТЪЃЛ
ЃЈ2ЃЉШєСНШЫГщШЁЕФЪ§зжКЭЮЊ4ЕФБЖЪ§ЃЌдђМзЛёЪЄЃЛШєГщШЁЕФЪ§зжКЭЮЊЦцЪ§ЃЌдђввЛёЪЄетгЮЯЗЙЋЦНТ№ЃПЧыгУИХТЪЕФжЊЪЖМгвдНтЪЭЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПБэжаЫљСа ![]() ЕФ7ЖджЕЪЧЖўДЮКЏЪ§
ЕФ7ЖджЕЪЧЖўДЮКЏЪ§![]() ЭМЯѓЩЯЕФЕуЫљЖдгІЕФзјБъЃЌЦфжа
ЭМЯѓЩЯЕФЕуЫљЖдгІЕФзјБъЃЌЦфжа ![]()
x | Ё |
|
|
|
|
|
|
| Ё |
y | Ё | 7 | m | 14 | k | 14 | m | 7 | Ё |
ИљОнБэжаЬсЙЉЕФаХЯЂЃЌгавдЯТ4 ИіХаЖЯЃК
Ђй ![]() ЃЛЂк
ЃЛЂк ![]() ЃЛЂл ЕБ
ЃЛЂл ЕБ![]() ЪБЃЌy ЕФжЕЪЧ kЃЛЂм
ЪБЃЌy ЕФжЕЪЧ kЃЛЂм ![]() ЦфжаХаЖЯе§ШЗЕФЪЧ ЃЈ ЃЉ
ЦфжаХаЖЯе§ШЗЕФЪЧ ЃЈ ЃЉ
A. ЂйЂкЂл B. ЂйЂкЂм C. ЂйЂлЂм D. ЂкЂлЂм
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com