
【题目】如图,AB为⊙O的直径,C是⊙O上一点,过点C的直线交AB的延长线于点D,AE⊥DC,垂足为E,F是AE与⊙O的交点,AC平分∠BAE. 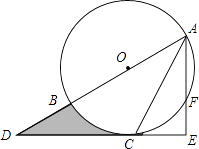
(1)求证:DE是⊙O的切线;
(2)若AE=6,∠D=30°,求图中阴影部分的面积.
【答案】
(1)证明:连接OC,
∵OA=OC,
∴∠OAC=∠OCA,
∵AC平分∠BAE,
∴∠OAC=∠CAE,
∴∠OCA=∠CAE,
∴OC∥AE,
∴∠OCD=∠E,
∵AE⊥DE,
∴∠E=90°,
∴∠OCD=90°,
∴OC⊥CD,
∵点C在圆O上,OC为圆O的半径,
∴CD是圆O的切线

(2)解:在Rt△AED中,
∵∠D=30°,AE=6,
∴AD=2AE=12,
在Rt△OCD中,∵∠D=30°,
∴DO=2OC=DB+OB=DB+OC,
∴DB=OB=OC= ![]() AD=4,DO=8,
AD=4,DO=8,
∴CD= ![]() =
= ![]() =4
=4 ![]() ,
,
∴S△OCD= ![]() =
= ![]() =8
=8 ![]() ,
,
∵∠D=30°,∠OCD=90°,
∴∠DOC=60°,
∴S扇形OBC= ![]() ×π×OC2=
×π×OC2= ![]() ,
,
∵S阴影=S△COD﹣S扇形OBC
∴S阴影=8 ![]() ﹣
﹣ ![]() ,
,
∴阴影部分的面积为8 ![]() ﹣
﹣ ![]()
【解析】(1)连接OC,先证明∠OAC=∠OCA,进而得到OC∥AE,于是得到OC⊥CD,进而证明DE是⊙O的切线;(2)分别求出△OCD的面积和扇形OBC的面积,利用S阴影=S△COD﹣S扇形OBC即可得到答案.
【考点精析】通过灵活运用切线的判定定理和扇形面积计算公式,掌握切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线;在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2)即可以解答此题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,D是△ABC的边BC上一点,AB=4,AD=2,∠DAC=∠B.如果△ABD的面积为15,那么△ACD的面积为( ) 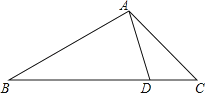
A.15
B.10
C.![]()
D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,AC=BC=2,正方形CDEF的顶点D,F分别在AC,BC边上,设CD的长度为x,△ABC与正方形CDEF重叠部分的面积为y,则下列图象中能表示y与x之间的函数关系的是( ) 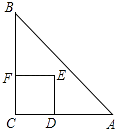
A.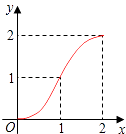
B.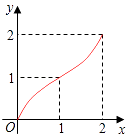
C.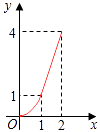
D.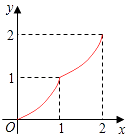
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料: 小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如:![]() ,善于思考的小明进行了以下探索:
,善于思考的小明进行了以下探索:
设![]() (其中
(其中![]() 均为整数),则有
均为整数),则有![]() .
.
∴![]() .这样小明就找到了一种把部分
.这样小明就找到了一种把部分![]() 的式子化为平方式的方法.
的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
当![]() 均为正整数时,若
均为正整数时,若![]() ,用含m、n的式子分别表示
,用含m、n的式子分别表示![]() ,得
,得![]() = ,
= ,![]() = ;
= ;
(2)利用所探索的结论,找一组正整数![]() ,填空: + =( +
,填空: + =( + ![]() )2;
)2;
(3)若![]() ,且
,且![]() 均为正整数,求
均为正整数,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小李从西安通过某快递公司给在南昌的外婆寄一盒樱桃,快递时,他了解到这个公司除收取每次6元的包装费外,樱桃不超过1kg收费22元,超过1kg,则超出部分按每千克10元加收费用.设该公司从西安到南昌快递樱桃的费用为y(元),所寄樱桃为x(kg).
(1)求y与x之间的函数关系式;
(2)已知小李给外婆快寄了2.5kg樱桃,请你求出这次快寄的费用是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】西安市在创建文明城区的活动中,有两个长度相等的彩色砖道铺设任务,分别交给甲、乙两个施工队同时进行施工,如图是反映所铺设的彩色砖道的长度y(米)与施工时间x(小时)之间关系的部分图象,请解答下列问题:
(1)求乙队在0≤x≤6的时段内y与x的函数关系式.
(2)如果甲队施工速度不变,乙队在施工6小时后,施工速度增加到12米/小时,结果两队同时完成了任务,求甲队从开始施工到完成所铺设的彩色砖道的长度为多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,AB=AC,∠BAC=90°,O为BC的中点。
(1)写出点O到△ABC的三个顶点A、B、C的距离的大小关系并说明理由;
(2)如果点M、N分别在线段AB、AC上移动,在移动中保持AN=BM,请判断△OMN的形状,并证明你的结论。
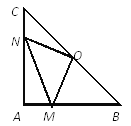
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com