
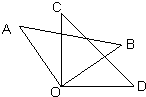
 27、如图所示,将两块三角板的顶点重合.
27、如图所示,将两块三角板的顶点重合.


科目:初中数学 来源:江苏期末题 题型:解答题

(1)如图1,当射线DF经过点B,即点Q与点B重合时,易证△APD~△CDQ。此时,AP·CQ=______。
(2)将三角板DEF由图1所示的位置绕点O沿逆时针方向旋转,设旋转角为a.其中 0°<a<90°,问AP·CQ的值是否改变?说明你的理由。
(3)在(2)的条件下,设CQ=x,两块三角板重叠面积为y,求y与x的函数关系式。(图2,图3供解题用)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com