
分析 (1)先去括号,把各根式化为最简二次根式,再合并同类项即可;
(2)先算括号里面的,再算除法,最后选出合适的x的值代入进行计算即可.
解答 解:(1)原式=2$\sqrt{3}$-$\frac{\sqrt{2}}{2}$-$\frac{\sqrt{2}}{4}$-$\sqrt{3}$
=$\sqrt{3}$-$\frac{3\sqrt{2}}{4}$;
(2)原式=$\frac{x}{(x+1)(x-1)}$÷$\frac{x}{x-1}$
=$\frac{x}{(x+1)(x-1)}$•$\frac{x-1}{x}$
=$\frac{1}{x+1}$,
当x=$\sqrt{2}$-1时,原式=$\frac{1}{\sqrt{2}-1+1}$=$\frac{\sqrt{2}}{2}$.
点评 本题考查的是分式的化简求值,此类题型的特点是:利用方程解的定义找到相等关系,再把所求的代数式化简后整理出所找到的相等关系的形式,再把此相等关系整体代入所求代数式,即可求出代数式的值.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
 梯形ABCD中,DC∥AB,DC=3,AB=4,E是DA的黄金分割点,且EF∥AB,则EF=$\frac{\sqrt{5}+5}{2}$.
梯形ABCD中,DC∥AB,DC=3,AB=4,E是DA的黄金分割点,且EF∥AB,则EF=$\frac{\sqrt{5}+5}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
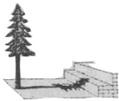 在阳光下,一名同学测得一根长为1米的垂直地面的竹竿的影长为0.6米,同时另一名同学测量树的高度时,发现树的影子不全落在地面上,有一部分落在教学楼的第一级台阶上,测得此影子长为0.2米,一级台阶高为0.3米,如图所示,若此时落在地面上的影长为4.42米,则树高为( )
在阳光下,一名同学测得一根长为1米的垂直地面的竹竿的影长为0.6米,同时另一名同学测量树的高度时,发现树的影子不全落在地面上,有一部分落在教学楼的第一级台阶上,测得此影子长为0.2米,一级台阶高为0.3米,如图所示,若此时落在地面上的影长为4.42米,则树高为( )| A. | 6.93米 | B. | 8米 | C. | 11.8米 | D. | 12米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在△ABC中,AB=6cm,AC=4cm,BD平分∠ABC,CD平分∠ACB,EF过点D且EF∥BC,则△AEF的周长是10cm.
如图,在△ABC中,AB=6cm,AC=4cm,BD平分∠ABC,CD平分∠ACB,EF过点D且EF∥BC,则△AEF的周长是10cm.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com