
【题目】如图,已知在Rt△ABC与Rt△ECD中,∠ACB=∠ECD=90°,CD为Rt△ABC斜边上的中线,且ED∥BC. 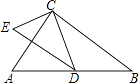
(1)求证:△ABC∽△EDC;
(2)若CE=3,CD=4,求CB的长.
【答案】
(1)证明:∵在Rt△ABC,CD为Rt△ABC斜边上的中线,
∴CD=BD,
∴∠DCB=∠B,
∵ED∥BC,
∴∠EDC=∠BCD,
∴∠B=∠EDC,
∵∠ACB=∠ECD=90°,
∴△ABC∽△EDC
(2)解:∵∠DCE=90°,CE=3,CD=4,
∴DE= ![]() =5,
=5,
∵在Rt△ABC,CD为Rt△ABC斜边上的中线,
∴AB=2CD=8,
∵△ABC∽△EDC,
∴ ![]() ,即
,即 ![]() ,
,
∴BC= ![]() .
.
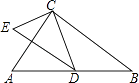
【解析】(1)根据直角三角形的性质得到CD=BD,由等腰三角形的性质得到∠DCB=∠B,根据平行线的性质得到∠EDC=∠BCD,等量代换得到∠B=∠EDC,根据相似三角形的判定定理即可得到结论;(2)根据勾股定理得到DE= ![]() =5,由直角三角形的性质得到AB=2CD=8,根据相似三角形的性质即可得到结论.
=5,由直角三角形的性质得到AB=2CD=8,根据相似三角形的性质即可得到结论.
【考点精析】解答此题的关键在于理解相似三角形的判定与性质的相关知识,掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y=2x+2的图象与y轴交于点B,与反比例函数y= ![]() 的图象的一个交点为A(1,m).过点B作AB的垂线BD,与反比例函数y=
的图象的一个交点为A(1,m).过点B作AB的垂线BD,与反比例函数y= ![]() (x>0)的图象交于点D(n,﹣2).
(x>0)的图象交于点D(n,﹣2).
(1)求k1和k2的值;
(2)若直线AB、BD分别交x轴于点C、E,试问在y轴上是否存在一个点F,使得△BDF∽△ACE?若存在,求出点F的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有下列四个结论:
①a÷m+a÷n=a÷(m+n);
② 某商品单价为a元。甲商店连续降价两次,每次都降10%。乙商店直接降20%。顾客选择甲或乙商店购买同样数量的此商品时,获得的优惠是相同的;
③若 ![]() ,则
,则 ![]() 的值为
的值为 ![]() ;
;
④关于x分式方程 ![]() 的解为正数,则
的解为正数,则 ![]() >1。
>1。
请在正确结论的题号后的空格里填“正确” ,在错误结论的题号后空格里填“错误”:
①; ②; ③; ④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=x2+bx+c与直线y=x交于(1,1)和(3,3)两点,现有以下结论:①b2﹣4c>0;
②3b+c+6=0;
③当x2+bx+c> ![]() 时,x>2;
时,x>2;
④当1<x<3时,x2+(b﹣1)x+c<0,
其中正确的序号是( )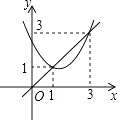
A.①②④
B.②③④
C.②④
D.③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,BC=AC,以BC为直径的⊙O与边AB、AC分别交于点D,E,DF⊥AC于点F. 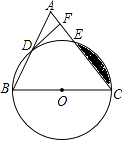
(1)求证:点D是AB的中点;
(2)判断DF与⊙O的位置关系,并证明你的结论;
(3)若⊙O的直径为20,cosB= ![]() ,求阴影部分面积.
,求阴影部分面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某校九年级3班的一个学习小组进行测量小山高度的实践活动.部分同学在山脚点A测得山腰上一点D的仰角为30°,并测得AD的长度为180米;另一部分同学在山顶点B测得山脚点A的俯角为45°,山腰点D的俯角为60度.请你帮助他们计算出小山的高度BC.(计算过程和结果都不取近似值)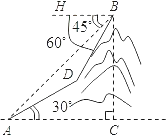
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com