
【题目】如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB. 
(1)求证:PC是⊙O的切线;
(2)求证:BC= ![]() AB;
AB;
(3)点M是 ![]() 的中点,CM交AB于点N,若AB=4,求MNMC的值.
的中点,CM交AB于点N,若AB=4,求MNMC的值.
【答案】
(1)证明:∵OA=OC,
∴∠A=∠ACO.
又∵∠COB=2∠A,∠COB=2∠PCB,
∴∠A=∠ACO=∠PCB.
又∵AB是⊙O的直径,
∴∠ACO+∠OCB=90°.
∴∠PCB+∠OCB=90°.
即OC⊥CP,
∵OC是⊙O的半径.
∴PC是⊙O的切线.
(2)证明:证明:∵AC=PC,
∴∠A=∠P,
∴∠A=∠ACO=∠PCB=∠P.
又∵∠COB=∠A+∠ACO,∠CBO=∠P+∠PCB,
∴∠COB=∠CBO,
∴BC=OC.
∴BC= ![]() AB.
AB.
(3)证明:解:连接MA,MB,
∵点M是 ![]() 的中点,
的中点,
∴ ![]() ,
,
∴∠ACM=∠BCM.
∵∠ACM=∠ABM,
∴∠BCM=∠ABM.
∵∠BMN=∠BMC,
∴△MBN∽△MCB.
∴ ![]() .
.
∴BM2=MNMC.
又∵AB是⊙O的直径, ![]() ,
,
∴∠AMB=90°,AM=BM.
∵AB=4,
∴BM=2 ![]() .
.
∴MNMC=BM2=8.

【解析】(1)已知C在圆上,故只需证明OC与PC垂直即可;根据圆周角定理,易得∠PCB+∠OCB=90°,即OC⊥CP;故PC是⊙O的切线;(2)AB是直径;故只需证明BC与半径相等即可;(3)连接MA,MB,由圆周角定理可得∠ACM=∠BCM,进而可得△MBN∽△MCB,故BM2=MNMC;代入数据可得MNMC=BM2=8.
【考点精析】本题主要考查了圆周角定理和切线的判定定理的相关知识点,需要掌握顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半;切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,∠A=90° 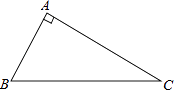
(1)请用圆规和直尺作出⊙P,使圆心P在AC边上,且与AB,BC两边都相切(保留作图痕迹,不写作法和证明).
(2)若∠B=60°,AB=3,求⊙P的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将边长为2的等边△OAB放置于平面直角坐标系xOy中,C是AB边上的一个点(不与端点A、B重合),作CD⊥OB于点D,若点C、D都在双曲线y= ![]() 上(k>0,x>0),则k的值为( )
上(k>0,x>0),则k的值为( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校准备购进一批节能灯,已知1只A型节能灯和3只B型节能灯共需26元;3只A型节能灯和2只B型节能灯共需29元.
(1)求一只A型节能灯和一只B型节能灯的售价各是多少元;
(2)学校准备购进这两种型号的节能灯共50只,并且A型节能灯的数量不多于B型节能灯数量的3倍,请设计出最省钱的购买方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AD=6,AB=4,点E、G、H、F分别在AB、BC、CD、AD上,且AF=CG=2,BE=DH=1,点P是直线EF、GH之间任意一点,连接PE、PF、PG、PH,则△PEF和△PGH的面积和等于 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,把两个全等的三角板ABC、EFG叠放在一起,使三角板EFG的直角边FG经过三角板ABC的直角顶点C,垂直AB于G,其中∠B=∠F=30°,斜边AB和EF均为4.现将三角板EFG由图1所示的位置绕G点沿逆时针方向旋转α(0°<α<90°),如图2,EG交AC于点K,GF交BC于点H.在旋转过程中,请你解决以下问题: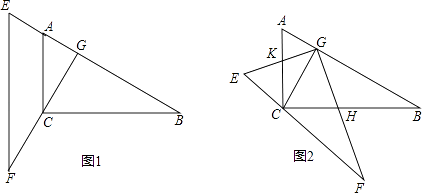
(1)求证:△CGH∽△AGK;
(2)连接HK,求证:KH∥EF;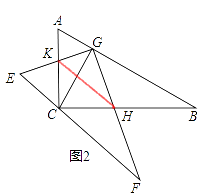
(3)设AK=x,△CKH的面积为y,求y关于x的函数关系式,并求出y的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把Rt△ABC和Rt△DEF按如图(1)摆放(点C与E重合),点B、C(E)、F在同一条直线上.已知:∠ACB=∠EDF=90°,∠DEF=45°,AC=8cm,BC=6cm,EF=10cm.如图(2),△DEF从图(1)的位置出发,以1cm/s的速度沿CB向△ABC匀速移动,在△DEF移动的同时,点P从△ABC的顶点A出发,以2cm/s的速度沿AB向点B匀速移动;当点P移动到点B时,点P停止移动,△DEF也随之停止移动.DE与AC交于点Q,连接PQ,设移动时间为t(s). 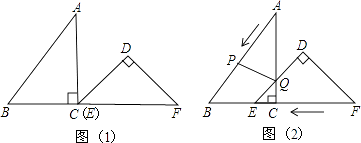
(1)用含t的代数式表示线段AP和AQ的长,并写出t的取值范围;
(2)连接PE,设四边形APEQ的面积为y(cm2),试探究y的最大值;
(3)当t为何值时,△APQ是等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系xOy中,点A、B的坐标分别为(3,0)、(2,﹣3),△AB′O′是△ABO关于点A的位似图形,且O′的坐标为(﹣1,0),则点B′的坐标为. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com