
【题目】如图,在平面直角坐标系中,将矩形AOCD沿直线AE折叠(点E在边DC上),折叠后端点D恰好落在边OC上的点F处.若点D的坐标为(10,8),则点E的坐标为 . 
【答案】(10,3)
【解析】解:∵四边形A0CD为矩形,D的坐标为(10,8), ∴AD=BC=10,DC=AB=8,
∵矩形沿AE折叠,使D落在BC上的点F处,
∴AD=AF=10,DE=EF,
在Rt△AOF中,OF= ![]() =6,
=6,
∴FC=10﹣6=4,
设EC=x,则DE=EF=8﹣x,
在Rt△CEF中,EF2=EC2+FC2 , 即(8﹣x)2=x2+42 , 解得x=3,
即EC的长为3.
∴点E的坐标为(10,3),
故答案为:(10,3).
根据折叠的性质得到AF=AD,所以在直角△AOF中,利用勾股定理来求OF=6,然后设EC=x,则EF=DE=8﹣x,CF=10﹣6=4,根据勾股定理列方程求出EC可得点E的坐标.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,将边长为6的正三角形纸片ABC按如下顺序进行两次折叠,展平后,得折痕AD,BE(如图①),点O为其交点.
(1)探求AO到OD的数量关系,并说明理由;
(2)如图②,若P,N分别为BE,BC上的动点.
(Ⅰ)当PN+PD的长度取得最小值时,求BP的长度;
(Ⅱ)如图③,若点Q在线段BO上,BQ=1,则QN+NP+PD的最小值= ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD与EFGH均为正方形,点B、F在函数y= ![]() (x>0)的图象上,点G、C在函数y=﹣
(x>0)的图象上,点G、C在函数y=﹣ ![]() (x<0)的图象上,点A、D在x轴上,点H、E在线段BC上,则点G的纵坐标 .
(x<0)的图象上,点A、D在x轴上,点H、E在线段BC上,则点G的纵坐标 . 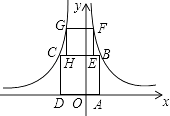
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某运动品牌专卖店准备购进甲、乙两种运动鞋.其中甲、乙两种运动鞋的进价和售价如下表.已知购进60双甲种运动鞋与50双乙种运动鞋共用10000元
运动鞋价格 | 甲 | 乙 |
进价(元/双) | m | m﹣20 |
售价(元/双) | 240 | 160 |
(1)求m的值;
(2)要使购进的甲、乙两种运动鞋共200双的总利润(利润=售价﹣进价)超过21000元,且不超过22000元,问该专卖店有几种进货方案?
(3)在(2)的条件下,专卖店准备决定对甲种运动鞋每双优惠a(50<a<70)元出售,乙种运动鞋价格不变.那么该专卖店要获得最大利润应如何进货?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,对角线AC、BD相交于点O,过点D作对角线BD的垂线交BA的延长线于点E. 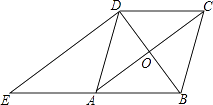
(1)证明:四边形ACDE是平行四边形;
(2)若AC=8,BD=6,求△ADE的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某林场计划购买甲、乙两种树苗共800株,甲种树苗每株24元,乙种树苗每株30元.相关资料表明:甲、乙两种树苗的成活率分别为85%、90%.
(1)若购买这两种树苗共用去21000元,则甲、乙两种树苗各购买多少株?
(2)若要使这批树苗的总成活率不低于88%,则甲种树苗至多购买多少株?
(3)在(2)的条件下,应如何选购树苗,使购买树苗的费用最低?并求出最低费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G,BG=4 ![]() ,则△CEF的周长为 .
,则△CEF的周长为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB为⊙O的直径,C、D是半圆的三等分点,延长AC,BD交于点E. 
(1)求∠E的度数;
(2)点M为BE上一点,且满足EMEB=CE2 , 连接CM,求证:CM为⊙O的切线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com