
【题目】在平面直角坐标系中,直线![]() :
:![]() 与直线
与直线![]() :
:![]() 且相交于点
且相交于点![]() ,直线
,直线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,直线
,直线![]() 与直线
与直线![]() ,
,![]() 分别相交于点
分别相交于点![]() 、
、![]() ,点
,点![]() 是线段
是线段![]() 的中点,以点
的中点,以点![]() 为顶点的抛物线
为顶点的抛物线![]() 经过点
经过点![]() .
.
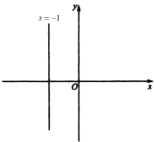
(1)①点![]() 的坐标是________;
的坐标是________;
②点![]() 的坐标是________.(用含
的坐标是________.(用含![]() 、
、![]() 的代数式表示)
的代数式表示)
(2)求![]() 的值(用含
的值(用含![]() 、
、![]() 的代数式表示);
的代数式表示);
(3)若![]() ,当
,当![]() 时,
时,![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)①![]() ,②
,②![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 的取值范围是
的取值范围是![]() 或
或![]() .
.
【解析】
(1)①由![]() 与x轴交于点B求得;
与x轴交于点B求得;
②根据直线![]() 与直线
与直线![]() ,
,![]() 分别相交于点
分别相交于点![]() 、
、![]() ,分别求出点C、D的坐标,利用点
,分别求出点C、D的坐标,利用点![]() 是线段
是线段![]() 的中点利用中点公式求出点P的纵坐标即可;
的中点利用中点公式求出点P的纵坐标即可;
(2)根据点P是抛物线的顶点设抛物线的解析式为![]() ,解方程组
,解方程组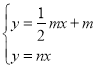 求出点A的坐标,再将点A的坐标代入抛物线的解析式即可求出a;
求出点A的坐标,再将点A的坐标代入抛物线的解析式即可求出a;
(3)由![]() 求出
求出![]() ,得到点
,得到点![]() 的坐标为
的坐标为![]() ,再分
,再分![]() 、
、![]() 两种情况分别求出m的取值范围.
两种情况分别求出m的取值范围.
(1)①∵![]() 与x轴交于点B,
与x轴交于点B,
∴当y=0时,得x=-2,
∴点B的坐标是(-2,0),
故答案为:![]() .
.
②∵直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,
,
∴当x=-1时,![]() =
=![]() ,
,
∴C(-1,![]() ),
),
∵直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,
,
∴当x=-1时,y=nx=-n,
∴D(-1,-n),
∴CD∥y轴,
∴点P的横坐标是-1,纵坐标是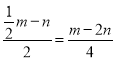 ,
,
故答案为:![]() .
.
(2)设抛物线的解析式为![]() .
.
![]() 直线
直线![]() :
:![]() 与直线
与直线![]() :
:![]() 交于点
交于点![]() ,
,
∴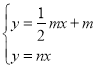 ,解得
,解得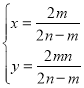 .
.
![]() 点
点![]() 的坐标是
的坐标是![]() .
.
![]() .
.
解得![]() .
.
(3)当![]() 时,
时,![]() .
.
![]() 抛物线解析式可以转化为
抛物线解析式可以转化为![]() .
.
![]() 点
点![]() 的坐标可以表示为
的坐标可以表示为![]() .
.
当![]() 时,抛物线开口向下,
时,抛物线开口向下,
![]() 当
当![]() 时,
时,![]() 有最大值,最大值为
有最大值,最大值为![]() .
.
![]() .解得
.解得![]() .
.
![]() .即
.即![]()
解得![]() .
.
当![]() 时,抛物线开口向上,
时,抛物线开口向上,
![]() 当
当![]() 时,
时,![]() 有最大值,最大值为
有最大值,最大值为![]() .
.
![]() .解得
.解得![]() .
.
![]() .即
.即![]() .
.
解得![]() .
.
综上,![]() 的取值范围是
的取值范围是![]() 或
或![]() .
.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源: 题型:
【题目】小字计划在某外卖网站点如下表所示的菜品,已知每份订单的配送费为3元,商家为了促销,对每份订单的总价(不含配送费)提供满减优惠:满30元减12元,满60元减30元,满100元减45元,如果小宇在购买下表中所有菜品时,采取适当的下订单方式,那么他点餐的总费用最低可为___元.
菜品 | 单价(含包装费) | 数量 |
| 30元 | 1 |
| 12元 | 1 |
| 30元 | 1 |
| 12元 | 1 |
| 3元 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,∠ACB=90°.
求作:射线CG,使得CG∥AB.
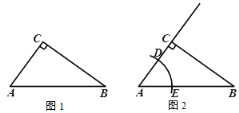
下面是小东设计的尺规作图过程.
作法:
①以点A为圆心,适当长为半径作弧,分别交AC,AB于D,E两点;
②以点C为圆心,AD长为半径作弧,交AC的延长线于点F;
③以点F为圆心,DE长为半径作弧,两弧在∠FCB内部交于点G;
④作射线CG.所以射线CG就是所求作的射线.
根据小东设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:连接FG、DE.
∵△ADE ≌ △_________,
∴∠DAE = ∠_________.
∴CG∥AB(___________________)(填推理的依据).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,直线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,与
,与![]() 轴相交于点
轴相交于点![]() ,以点
,以点![]() 为圆心,线段
为圆心,线段![]() 的长为半径画弧,与直线
的长为半径画弧,与直线![]() 位于第一象限的部分相交于点
位于第一象限的部分相交于点![]() ,则点
,则点![]() 的坐标为_______.
的坐标为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
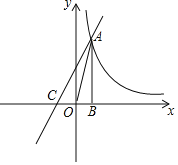
【题目】如图,已知反比例函数y=![]() 的图象经过第一象限内的一点A(n,4),过点A作AB⊥x轴于点B,且△AOB的面积为2.
的图象经过第一象限内的一点A(n,4),过点A作AB⊥x轴于点B,且△AOB的面积为2.
(1)求m和n的值;
(2)若一次函数y=kx+2的图象经过点A,并且与x轴相交于点C,求线段AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD⊥BC于点D,点F为AB上一点,连接CF,过点B作BE⊥BC交CF的延长线于点E,交AD于点H,且∠1=∠2
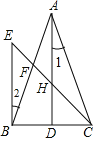
(1)求证:AB=AC;
(2)若∠1=22°,∠AFC=110°,求∠BCE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为改善办学条件,计划购进![]() 两种规格的书架,经市场调查发现有线下和线上两种方式,具有情况如下表:
两种规格的书架,经市场调查发现有线下和线上两种方式,具有情况如下表:
规格 | 线下 | 线上 | ||
单价(元/个) | 运费(元/个) | 单价(元/个) | 运费(元/个) | |
A | 240 | 0 | 210 | 20 |
B | 300 | 0 | 250 | 30 |
(Ⅰ)如果在线下购买![]() 两种书架20个,共花费5520元,求
两种书架20个,共花费5520元,求![]() 两种书架各购买了多少个;
两种书架各购买了多少个;
(Ⅱ)如果在线上购买![]() 两种书架20个,共花费
两种书架20个,共花费![]() 元,设其中
元,设其中![]() 种书架购买
种书架购买![]() 个,求W关于
个,求W关于![]() 的函数关系式;
的函数关系式;
(Ⅲ)在(Ⅱ)的条件下,若购买![]() 种书架的数量不少于
种书架的数量不少于![]() 种书架的2倍,请求出花费最少的购买方案,并计算按照该购买方案线上比线下节约多少钱.
种书架的2倍,请求出花费最少的购买方案,并计算按照该购买方案线上比线下节约多少钱.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 是线段
是线段![]() 上一点,
上一点,![]() ,以点
,以点![]() 为圆心,
为圆心,![]() 的长为半径作⊙
的长为半径作⊙![]() ,过点
,过点![]() 作
作![]() 的垂线交⊙
的垂线交⊙![]() 于
于![]() ,
,![]() 两点,点
两点,点![]() 在线段
在线段![]() 的延长线上,连接
的延长线上,连接![]() 交⊙
交⊙![]() 于点
于点![]() ,以
,以![]() ,
,![]() 为边作
为边作![]() .
.

(1)求证:![]() 是⊙
是⊙![]() 的切线;
的切线;
(2)若![]() ,求四边形
,求四边形![]() 与⊙
与⊙![]() 重叠部分的面积;
重叠部分的面积;
(3)若![]() ,
,![]() ,连接
,连接![]() ,求
,求![]() 和
和![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com