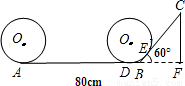
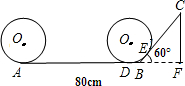
解:(1)由圆的半径10cm,得到圆的周长C=2πr=20π≈62.8cm,
所以当圆盘在AB上滚动一圈时,求其圆心所经过的路线长度是62.8cm;
(2)连接OD和OB,根据切线性质得到∠ODB=90°,∠DOB=30°,
设BD=xcm,则OB=2xcm,根据勾股定理得:DB
2+OD
2=OB
2,
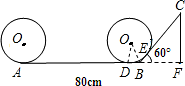
即x
2=

,
解得x=

,
即BD=

cm,
所以当圆盘从A点滚到与BC开始相切时,其圆心O所经过的路线长是AD=AB-BD=80-

≈74.2cm;
(3)由切线性质得:BD=BE=

cm,
在直角△BCF中,∠CBF=60°,CF=30cm,
则BC=
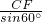
=20

cm,
所以切点E到顶端C的距离为20

-

=28.9cm.
分析:(1)当圆盘在AB上滚动一圈时,其圆心所经过的路线长为圆的周长,所以由圆的半径求出圆的周长即可;
(2)当圆盘从A点滚到与BC开始相切时,连接OD和OB,根据切线性质得到三角形OBD为直角三角形且角OBD为60°,设BD=x,根据勾股定理即可列出关于x的方程,求出x的值得到BD的长,用AB-BD即可求出AD的长即为其圆心O所经过的路线长是AD的长度;
(3)在直角三角形CBF中,由CF的长和角CBF的度数,利用三角函数,即可求出BC的长,根据(2)中求出的BD长得到EB的长,利用BC-BE即可求出EC的长.
点评:此题考查学生掌握圆切线的性质即圆外一点作圆的两条切线,切线长相等且圆心与这点的连线平分两切线的夹角,灵活运用勾股定理及三角函数的定义化简求值,考查学生将实际问题转化为数学问题的能力,培养学生识别图形的能力,让学生了解数学来自于生活,又服务于生活的理念.

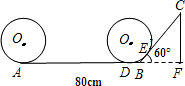 cm)
cm)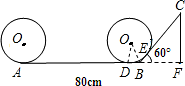
 ,
, ,
, cm,
cm, ≈74.2cm;
≈74.2cm; cm,
cm,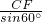 =20
=20 cm,
cm, -
- =28.9cm.
=28.9cm.

 cm)
cm)