
����Ŀ����ͼ����������������A��B����![]() ��ʾ����Ϊ6����B�ڵ�A����࣬��AB=20������P�ӵ�A��������ÿ��4����λ���ȵ��ٶ����������������˶������˶�ʱ��Ϊt�루t>0��.
��ʾ����Ϊ6����B�ڵ�A����࣬��AB=20������P�ӵ�A��������ÿ��4����λ���ȵ��ٶ����������������˶������˶�ʱ��Ϊt�루t>0��.
![]()
��1��д�������ϵ�B��ʾ����______����P��ʾ�����ú�t��ʽ�ӱ�ʾ��_______��
��2�����M��AP���е㣬��N��PB���е�.��P��ֱ��AB���˶��Ĺ����У��߶�MN�ij����Ƿ�ᷢ���仯���������仯����˵�����ɣ������仯������߶�MN�ij���.
��3������R�ӵ�B��������ÿ��2����λ���ȵ��ٶ����������������˶�������P��Rͬʱ����������P�˶�������ʱ�����R�ľ���Ϊ2����λ����.
���𰸡���1��-14��6-4t����2���߶�MN�ij��Ȳ������仯��MN�ij���Ϊ10cm����3����P�˶�11���9��ʱ�����R�ľ���Ϊ2����λ����.
��������
��1�����ݵ�B�ڵ�A����༰�������������빫ʽ���ɵó���B��ʾ���������þ���=�ٶ���ʱ��ɱ�ʾAP�ľ��룬���ɱ�ʾ����P��ʾ������
��2�������е�Ķ�������AM��BN�ij�������MN=AB-BN-AM�������MN�ij������ɵô𰸣�
��3�����þ���=�ٶ���ʱ��ɵó���R�͵�P��ʾ�����������������������빫ʽ�з������tֵ����.
��1���ߵ�![]() ��ʾ����Ϊ6����B�ڵ�A����࣬��AB=20��
��ʾ����Ϊ6����B�ڵ�A����࣬��AB=20��
���B��ʾ����Ϊ6-20=-14��
�߶���P�ӵ�A��������ÿ��4����λ���ȵ��ٶ����������������˶���
���P��ʾ����Ϊ6-4t��
�ʴ�Ϊ��-14��6-4t
��2����ͼ���ߵ�M��AP���е㣬��P���ٶ�Ϊÿ��4����λ���ȣ�
��AM=![]() ��4t=2t��
��4t=2t��
�ߵ�N��PB���е㣬
��BN=![]() ��(20-4t)=10-2t��
��(20-4t)=10-2t��
��MN=AB-BN-AM=20-(10-2t)-2t=10��
![]()
���P��ֱ��AB���˶��Ĺ����У��߶�MN�ij��Ȳ������仯��MN�ij���Ϊ10cm.
��3���߶���R�ӵ�B��������ÿ��2����λ���ȵ��ٶ����������������˶���
���R��ʾ������-14-2t��
�ߵ�P��ʾ����Ϊ6-4t����P���R�ľ���Ϊ2����λ����.
��PR=![]() =2����
=2����![]() =2��
=2��
��ã�t=11��t=9��
���P�˶�11���9��ʱ�����R�ľ���Ϊ2����λ����.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ݱ��أ��ڡ������ͥ��̼�У���������Ҫ���С���У�ij�����������ȡ��1000�����������ηֲ�����Ͷ�������������̬�Ƚ��е��飬�����������ֱ�������ͼ������ͼ��
��1��ͼ2����ȱ�ٵİٷ�����____________��
��2�������������У�������ǡ�25�����¡��Ĺ����С����ɡ�����5������ռ��25�����¡������İٷ�����_____________��
��3�����������̬���еġ�����ͬ���͡���ͬ��ͳ��Ϊ��֧�֡�����ô��α����鹫���С�֧�֡�������_______________����


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У������P �ĺ��������������ȣ���Ƶ�PΪ��г�㡣
��1������![]() ��ͼ���Ϻ�г������ꣻ
��ͼ���Ϻ�г������ꣻ
��2�������κ���y��ax2+4x+c��a��0����ͼ��������ֻ��һ����г�㣨![]() ��
��![]() ������0��x��mʱ������y��ax2+4x+c��
������0��x��mʱ������y��ax2+4x+c��![]() ��a��0������СֵΪ��3�����ֵΪ1����m��ȡֵ��Χ.
��a��0������СֵΪ��3�����ֵΪ1����m��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���ACB=900����B����A����DΪ��AB���е㣬DE��BC��AC�ڵ�E��CF��AB��DE���ӳ����ڵ�F��

��1����֤��DE=EF��
��2������CD������D��DC�Ĵ��߽�CF���ӳ����ڵ�G����֤����B=��A����DGC��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����2017����ʡ̩���У���25�⣬12�֣��Ķ����⣺
��ͼ�٣�ͼ��l��һ��P��ͼ��l�ϸ������ӵ������߶��У����߶�PA1��̣����߶�PA1�ij��ȳ�Ϊ��P��ͼ��l�ľ��룮
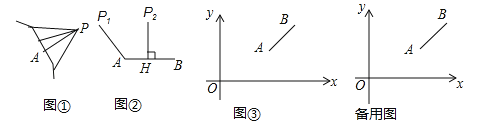
���磺ͼ���У��߶�P1A�ij����ǵ�P1���߶�AB�ľ��룻�߶�P2H�ij����ǵ�P2���߶�AB�ľ��룮
������⣺
��ͼ�ۣ�ƽ��ֱ������ϵxOy�У���A��B������ֱ�Ϊ��8��4������12��7������P��ԭ��O��������ÿ��1����λ���ȵ��ٶ���x���������˶���t�룮
��1����t=4ʱ�����P���߶�AB�ľ��룻
��2��tΪ��ֵʱ����P���߶�AB�ľ���Ϊ5��
��3��t����ʲô����ʱ����P���߶�AB�ľ��벻����6����ֱ��д����С��Ľ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������ϵĵ�A��B��C��D��E��Ӧ�����ֱ�Ϊa��b��c��d��e��
![]()
��1������|a��c|��2|b��a|��|b��c|��
��2���������������ÿ����������֮��ľ��붼��ȣ���|a|��|e|��|b|��3��ֱ��д��b��e��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵����������������Ϊ�����������ǵij˻�Ϊ1������a��b��Ϊ�෴������![]() ����1���۶���ʽ
����1���۶���ʽ![]() �Ĵ���Ϊ4������aΪ��������������
�Ĵ���Ϊ4������aΪ��������������![]() ��0��������ȷ���� �� ��
��0��������ȷ���� �� ��
A.1��B.2��C.3��D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����ÿ��������Ҫ����һ��Ѫѹ���±��Ǹò��˱�������һ������������ѹ�ı仯���.����������ʾ��������������ʾ�½���
���� | һ | �� | �� | �� | �� |
����ѹ�ı仯����ǰһ��Ƚϣ� | +30 | -20 | +17 | +18 | -20 |
��1������������һ��Ƚ�����ѹ________�ˣ�������������½�����
��2��ͨ������˵������������ѹ������������������˻����½��ˣ�������������½��˶��٣�
��3������ò��˱����������ѹΪ185����ô���ϸ����յ�����ѹΪ���٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��1883�꣬���ж������������Σ��������ж������ӳ���Ϊ1���߶ο�ʼ�����ж�ȡ�����м�����֮һ���ﵽ��һ�Σ�Ȼ���ÿ�˸����µ�����֮һ�߶���ȡ���м�����֮һ���ﵽ�ڶ��Σ������ظ���һ���̣����µ������ͳ������ж�������ͼ�ǿ��ж�������������Σ����ﵽ��5����ʱ��ȡ�ߵ������߶εij���֮��Ϊ�� ��

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com