
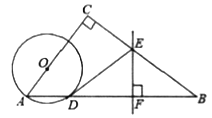
【题目】如图在![]() 中,
中,![]() ,点
,点![]() 在
在![]() 上,以
上,以![]() 为半径的⊙
为半径的⊙![]() 交
交![]() 于
于![]() ,
,![]() 的垂直平分线交
的垂直平分线交![]() 于
于![]() ,交
,交![]() 于
于![]() ,连接
,连接![]() .
.
(1)求证:![]() 是⊙
是⊙![]() 的切线;
的切线;
(2)若![]() ,
,![]() ,且
,且![]() ,求⊙
,求⊙![]() 的直径.
的直径.
【答案】(1)证明见解析;(2)⊙O的直径为![]()
【解析】
(1)直线DE与圆O相切,理由如下:连接OD,由OD=OA,利用等边对等角得到一对角相等,等量代换得到∠ODE为直角,即可得证;
(2)利用∠B=30°,BC=4![]() ,且AD:DF=1:2,求得AD的长,再根据△AOD是等边三角形,可得AO=AD=
,且AD:DF=1:2,求得AD的长,再根据△AOD是等边三角形,可得AO=AD=![]() ,进而得到⊙O的直径为
,进而得到⊙O的直径为![]() .
.
解:(1)如图,连接OD,
∵OD=OA, ∴∠A=∠ODA,
∵EF是BD的垂直平分线, ∴EB=ED, ∴∠B=∠EDB,
∵∠C=90°,∴∠A+∠B=90°,∴∠ODA+∠EDB=90°,
∴∠ODE= 180°(∠ODA+∠EDB)=180°90°=90°,
∴OD⊥DE于E又∵OD是⊙O的半径
∴直线DE与⊙O相切;
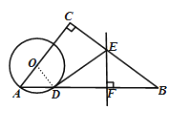
(2)∵∠B=30°,∴∠A=180°-∠B-∠C=60°
∵OD=OA ∴△OAD是等边三角形
在Rt△ABC中,设AC=x,则AB=2x,
AC2+BC2=AB2,即![]() 解得x=4,∴AC=4,则AB=8
解得x=4,∴AC=4,则AB=8
设AD =m,则DF=BF=2m,
∵AB=AD+2DF即m+4m=8,得m=![]()
∴OA=AD=![]() ,2OA =
,2OA =![]()
答:⊙O的直径为![]()


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
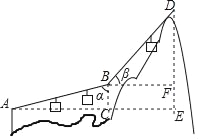
【题目】如图,游客在点A处坐缆车出发,沿A﹣B﹣D的路线可至山顶D处.已知AB=BD=800米,∠α=75°,∠β=45°,求山高DE(结果精确到1米).(参考数据:sin75°=0.966,cos75°=0.259,tan75°=3.732,![]() =1.414)
=1.414)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明想利用太阳光测量楼高,他带着皮尺来到一栋楼下,发现对面墙上有这栋楼的影子,针对这种情况,他设计了一种测量方案,具体测量情况如下:如示意图,小明边移动边观察,发现站到点E处时,可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠,且高度恰好相同.此时,测得小明落在墙上的影子高度CD=1.2m,CE=0.8m,CA=30m(点A、E、C在同一直线上).已知小明的身高EF是1.7m,请你帮小明求出楼高AB(结果精确到0.1m).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】附加题:如图,直线![]() :
:![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 、
、![]() ,经过
,经过![]() 、
、![]() 两点的抛物线
两点的抛物线![]() 与
与![]() 轴的另一个交点为
轴的另一个交点为![]() .
.
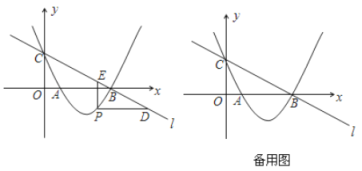
(1)求该抛物线的解析式;
(2)若点![]() 在直线
在直线![]() 下方的抛物线上,过点
下方的抛物线上,过点![]() 作
作![]() 轴交
轴交![]() 于点
于点![]() ,
,![]() 轴交
轴交![]() 于点
于点![]() ,求
,求![]() 的最大值;
的最大值;
(3)设![]() 为直线
为直线![]() 上的点,以
上的点,以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形能否构成平行四边形?若能,求出点
为顶点的四边形能否构成平行四边形?若能,求出点![]() 的坐标;若不能,请说明理由.
的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
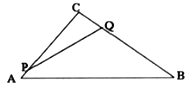
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 从点
从点![]() 沿
沿![]() 向点
向点![]() 以
以![]() 的速度运动,同时点
的速度运动,同时点![]() 从点
从点![]() 沿
沿![]() 向点
向点![]() 以
以![]() 的速度运动(点
的速度运动(点![]() 运动到点
运动到点![]() 停止),在运动的过程中,四边形
停止),在运动的过程中,四边形![]() 的面积的最小值为__________
的面积的最小值为__________![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线C:y=-x2+bx+c经过A(-3,0)和B(0,3)两点,将这条抛物线的顶点记为M,它的对称轴与x轴的交点记为N.
(1)求抛物线C的表达式;
(2)求点M的坐标;
(3)将抛物线C平移到抛物线C′,抛物线C′的顶点记为M′,它的对称轴与x轴的交点记为N′.如果以点M、N、M′、N′为顶点的四边形是面积为16的平行四边形,那么应将抛物线C怎样平移?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,斜坡AB长10米,按图中的直角坐标系可用y=![]() x+5表示,点A,B分别在x轴和y轴上.在坡上的A处有喷灌设备,喷出的水柱呈抛物线形落到B处,抛物线可用y=
x+5表示,点A,B分别在x轴和y轴上.在坡上的A处有喷灌设备,喷出的水柱呈抛物线形落到B处,抛物线可用y=![]() x2+bx+c表示.
x2+bx+c表示.
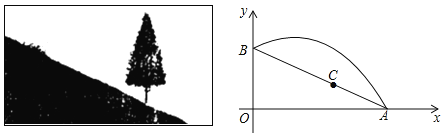
(1)求抛物线的函数关系式(不必写自变量取值范围);
(2)求水柱离坡面AB的最大高度;
(3)在斜坡上距离A点2米的C处有一颗3.5米高的树,水柱能否越过这棵树?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,AD的中点,
且∠ABM=∠BAM,连接BM,MN,BN.
(1)求证:BM=MN;
(2)∠BAD=60°,AC平分∠BAD,AC=2,求BN的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com