
 (1)如图锐角的正弦值和余弦值都随着锐角的确定而确定,变化而变化,试探索随着锐角度数的增大,它的正弦值和余弦值变化的规律.
(1)如图锐角的正弦值和余弦值都随着锐角的确定而确定,变化而变化,试探索随着锐角度数的增大,它的正弦值和余弦值变化的规律. ,sin∠B2AC=
,sin∠B2AC=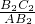 ,sin∠B3AC=
,sin∠B3AC=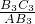 ,
, >
>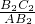 >
>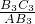 ,
, ,cos∠B2AC=
,cos∠B2AC= ,cos∠B3AC=
,cos∠B3AC= ,
, >
> >
> .
.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
 (1)如图,在锐角三角形ABC中,BC=12,sinA=
(1)如图,在锐角三角形ABC中,BC=12,sinA=| 3 | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
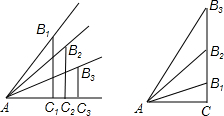 (1)如图锐角的正弦值和余弦值都随着锐角的确定而确定,变化而变化,试探索随着锐角度数的增大,它的正弦值和余弦值变化的规律.
(1)如图锐角的正弦值和余弦值都随着锐角的确定而确定,变化而变化,试探索随着锐角度数的增大,它的正弦值和余弦值变化的规律.查看答案和解析>>
科目:初中数学 来源:2009-2010学年安徽省滁州市五中九年级(上)期末复习数学试卷(六)(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2010-2011学年山东省济宁市邹城八中九年级(上)摸底考试数学试卷几何部分(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com