
分析 (1)根据题意算式确定出第10个和第n个算式即可;
(2)将a、b的值代入原式,原式利用拆项法变形,计算即可得到结果.
解答 解:(1)根据题意,第10个算式为$\frac{1}{1×11}$=$\frac{1}{10}$×(1-$\frac{1}{11}$),
第n个等式为$\frac{1}{1×(n+1)}$=$\frac{1}{n}×$(1-$\frac{1}{n+1}$),
故答案为:$\frac{1}{1×11}$,$\frac{1}{10}$×(1-$\frac{1}{11}$),$\frac{1}{1×(n+1)}$,$\frac{1}{n}×$(1-$\frac{1}{n+1}$),
(2)根据题意知,a=1,b=3.
原式=$\frac{1}{1×3}$+$\frac{1}{3×5}$+$\frac{1}{5×7}$+…+$\frac{1}{101×103}$
=$\frac{1}{2}$(1-$\frac{1}{3}$)+$\frac{1}{2}$($\frac{1}{3}$-$\frac{1}{5}$)+$\frac{1}{2}$($\frac{1}{5}$-$\frac{1}{7}$)+…+$\frac{1}{2}$($\frac{1}{101}$-$\frac{1}{103}$)
=$\frac{1}{2}$(1-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{5}$+$\frac{1}{5}$-$\frac{1}{7}$+…+$\frac{1}{101}$-$\frac{1}{103}$)
=$\frac{1}{2}$(1-$\frac{1}{103}$)
=$\frac{1}{2}$×$\frac{102}{103}$
=$\frac{51}{103}$.
点评 此题考查了数字的变化规律和有理数的混合运算,熟练掌握运算法则是解本题的关键.


 优生乐园系列答案
优生乐园系列答案科目:初中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | 2 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
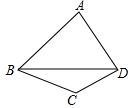 如图四边形ABCD中,∠ABC=3∠CBD,∠ADC=3∠CDB,∠C=128°,则∠A的度数是( )
如图四边形ABCD中,∠ABC=3∠CBD,∠ADC=3∠CDB,∠C=128°,则∠A的度数是( )| A. | 60° | B. | 76° | C. | 77° | D. | 78° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,其中A点坐标为(-1,0),点C(0,5),另抛物线经过点(1,8),M为它的顶点.
已知:如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,其中A点坐标为(-1,0),点C(0,5),另抛物线经过点(1,8),M为它的顶点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com