
����С������12�֣���ͼ���ı���OABCΪֱ�����Σ�A��4��0����B��3��4����C��0��4������M��O������ÿ��2����λ���ȵ��ٶ���A�˶�����N��Bͬʱ��������ÿ��1����λ���ȵ��ٶ���C�˶�������һ�����㵽���յ�ʱ����һ������Ҳ��ֹ֮ͣ�˶�������N��NP��ֱx���ڵ�P������AC��NP��Q������MQ��

��1���� ����M��N���ܵ����յ㣻
��2�����AQM�����S���˶�ʱ��t�ĺ�����ϵʽ����д���Ա���t��ȡֵ��Χ����tΪ��ֵʱ��S��ֵ���
��3���Ƿ���ڵ�M��ʹ�á�AQMΪֱ�������Σ������ڣ������M�����ꣻ�������ڣ�˵�����ɣ�
��1��M����2��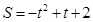
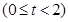 ����
����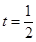 ʱ��S��ֵ���3�����ڣ���M������Ϊ��1��0����2��0�������ɼ����������
ʱ��S��ֵ���3�����ڣ���M������Ϊ��1��0����2��0�������ɼ����������
��������
�����������1����BC�µ�N���˶��ٶȣ��루OA�µ�M���˶��ٶȣ���֪��M�ܵ����յ㣮
��2������t��ʱ�ɵ�NB=y��OM��2t�����ݡ�BCA=��MAQ=45���Ƴ�QN=CN��PQ��ֵ�����S��t�ĺ�����ϵʽ�����t��ֵ���S�����ֵ��
��3�����������������ۣ�����AQM=90�㣬PQ�ǵ���Rt��MQA�ױ�MA�ϵĸߣ�����QMA=90�㣬QM��QP�غϣ����tֵ��
�����������1����M��
��2������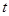 ��ʱ��NB=
��ʱ��NB=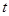 ��OM=
��OM=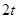 ����CN=
����CN=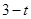 ��AM=
��AM=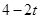 ����A��4��0����C��0��4������AO=CO=4���ߡ�AOC=90�㣬���BCA=��MAQ=45�㣬��QN=CN=
����A��4��0����C��0��4������AO=CO=4���ߡ�AOC=90�㣬���BCA=��MAQ=45�㣬��QN=CN=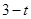 ����PQ=
����PQ=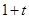 ��
��
��S��AMQ=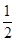 AM•PQ=
AM•PQ= =
=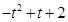 ����
����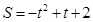 ����
����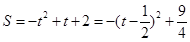 ����
����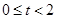 ���൱
���൱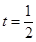 ʱ��S��ֵ���
ʱ��S��ֵ���
��3�����ڣ�
�辭��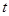 ��ʱ��NB=
��ʱ��NB=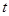 ��OM=
��OM=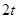 ����CN=
����CN=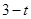 ��AM=
��AM=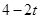 �����BCA=��MAQ=45�㣮
�����BCA=��MAQ=45�㣮
������AQM=90�㣬��PQ�ǵ���Rt��MQA�ױ�MA�ϵĸߣ���PQ�ǵױ�MA�����ߣ���PQ=AP=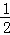 MA��
MA��
��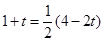 ����
����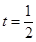 �����M��������1��0����
�����M��������1��0����
������QMA=90�㣬��ʱQM��QP�غϣ���QM=QP=MA����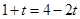 ����ã�
����ã�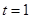 �����M������Ϊ��2��0����
�����M��������2��0����

���㣺���κ����ۺ��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2011-2012ѧ����꼶�ڶ���ģ�⿼����ѧ�� ���ͣ������
����С������12�֣�
��ͼ������������ ��ͼ��A��B���㣬����ͼ����Ϣ����������⣺
��ͼ��A��B���㣬����ͼ����Ϣ����������⣺

1.��1��д��A������ꣻ
2.��2�����������Ľ���ʽ��
3.��3������A������ԭ��O��ת90���õ���C����д����C�����ꣻ�����ֱ��BC�Ľ���ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2011-2012��ӱ�ʡ��ˮ����У���꼶������������ѧ�� ���ͣ������
����С������12�֣�
��ͼ��1������ABC���EFDΪ����ֱ�������Σ�AC��DE�غϣ�AB=EF=9����BAC����DEF��90�㣬�̶���ABC������EFD�Ƶ�A ˳ʱ����ת����DF����AB���غ�ʱ����ת��ֹ����������ת��ʼ�ͽ���ʱ�غϵ��������DE��DF�������ǵ��ӳ��ߣ��ֱ�BC���������ӳ��ߣ���G��H�㣬��ͼ��2����

1.��1���ʣ�ʼ�����AGC���Ƶ��������� �� ��
2.��2����CG��x��BH��y����y����x�ĺ�����ϵʽ��ֻҪ�����2�����˵�����ɣ���
3.��3���ʣ���xΪ��ֵʱ����AGH�ǵ��������Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2011-2012��ӱ�ʡ��ˮ����У���꼶������������ѧ�� ���ͣ������
����С������12�֣�ij��ͬѧ��Ұ����Ϊ����һ��������A��B�ľ��룬����˼��ַ���������������֣���I����ͼ��1��������ƽ��ȡһ������ֱ�ӵ���A��B�ĵ�C�����ֱ��ӳ�AC��D��BC��E��ʹDC=AC��BC=EC�������DE�ľ��뼴ΪAB�ij�����II����ͼ��2�����ȹ�B����AB�Ĵ���BF������BF��ȡC��D���㣬ʹBC=CD�����Ź���D��BD�Ĵ���DE����AC���ӳ�����E������DE�ij���ΪAB�ľ��롣�Ķ���ش��������⣺

1.��1��������I���Ƿ���У�Ϊʲô��
2.��2��������II���Ƿ���ʵ���У�Ϊʲô��
3.��3��������II������BF��AB��ED��BF��Ŀ���� �����������ABD=��BDE��90�㣬������II���Ƿ������
4.��4��������II���У���ʹBC=n��CD���ܷ��ã��������AB�ij��������� ����ED=m����AB= ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2011-2012�꽭��GSJY���꼶�ڶ���ѧ����п�����ѧ�� ���ͣ������
(��������12��)
1. (1)�۲췢��
��(a)ͼ������A��B��ֱ�� ͬ�࣬��ֱ��
ͬ�࣬��ֱ�� ����һ��P��ʹAP+BP��ֵ��С��
����һ��P��ʹAP+BP��ֵ��С��
�������£�����B����ֱ�� �ĶԳƵ�
�ĶԳƵ� ������
������ ����ֱ��
����ֱ�� �Ľ����������ĵ�P
�Ľ����������ĵ�P
����(b)ͼ���ڵȱ�������ABC�У�AB=2����E��AB���е㣬AD�Ǹߣ���AD����һ��P��ʹBP+PE��ֵ��С��
�������£�����B����AD�ĶԳƵ㣬ǡ�����C�غϣ�����CE��AD��һ�㣬������������ĵ�P����BP+PE����СֵΪ �� (2��)

2.(2)ʵ������
��ͼ������ABCD�������Խ��߷ֱ�6��8����P�ǶԽ���AC�ϵ�һ�����㣬��M��N�ֱ��DZ�AB��BC���е㣬��PM+PN����Сֵ��(5��)

3.(3)��չ����
��(d)ͼ�����ı���ABCD�ĶԽ���AC����һ��P��ʹ��APB=��APD��������ͼ�ۼ�������д�������� (5��)

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014�����ʡТ�������꼶��ѧ�����п�����ѧ�� ���ͣ������
������С������12�֣�
��ͼ��ADΪ��ABC�����ߣ�BEΪ��ABD�����ߡ�

��1����ABE=15�㣬��BAD=40�㣬���BED�Ķ�����
��2���ڡ�BED����BD���ϵĸߣ�
��3������ABC�����Ϊ40��BD=5�����BDE ��BD���ϵĸ�Ϊ���٣�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com