
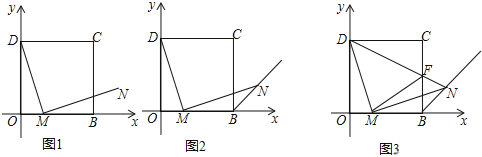
【题目】(1)如图,在平面直角坐标系中,四边形OBCD是正方形,且D(0,2),点E是线段OB延长线上一点,M是线段OB上一动点(不包括点O、B),作MN⊥DM,垂足为M,且MN=DM.设OM=a,请你利用基本活动经验直接写出点N的坐标______(用含a的代数式表示);
(2)如果(1)的条件去掉“且MN=DM”,加上“交∠CBE的平分线与点N”,如图,求证:MD=MN.如何突破这种定势,获得问题的解决,请你写出你的证明过程.
(3)在(2)的条件下,如图,请你继续探索:连接DN交BC于点F,连接FM,下列两个结论:①FM的长度不变;②MN平分∠FMB,请你指出正确的结论,并给出证明.
【答案】(1)(2+a,a);(2)证明见解析;(3)②MN平分∠FMB成立,证明见解析.
【解析】
(1)如图1中,作NE⊥OB于E,只要证明△DMO≌△MNE即可解决问题.
(2)如图2中,在OD上取OH=OM,连接HM,只要证明△DHM≌△MBN即可.
(3)结论:MN平分∠FMB成立.如图3中,在BO延长线上取OA=CF,过M作MP⊥DN于P,因为∠NMB+∠CDF=45°,所以只要证明∠FMN+∠CDF=45°即可解决问题.
(1)解:如图1中,作NE⊥OB于E,
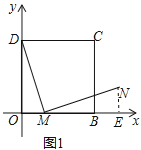
∵∠DMN=90°,
∴∠DMO+∠NME=90°,∠NME+∠MNE=90°,
∴∠DMO=∠MNE,
在△DMO和△MNE中,
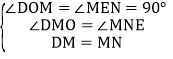 ,
,
∴△DMO≌△MNE,
∴ME=DO=2,NE=OM=a,
∴OE=OM+ME=2+a,
∴点N坐标(2+a,a),
故答案为N(2+a,a).
(2)证明:如图2中,在OD上取OH=OM,连接HM,
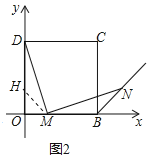
∵OD=OB,OH=OM,
∴HD=MB,∠OHM=∠OMH=45°,
∴∠DHM=180°-45°=135°,
∵NB平分∠CBE,
∴∠NBE=45°,
∴∠NBM=180°-45°=135°,
∴∠DHM=∠NBM,
∵∠DMN=90°,
∴∠DMO+∠NMB=90°,
∵∠HDM+∠DMO=90°,
∴∠HDM=∠NMB,
在△DHM和△MBN中,
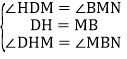 ,
,
∴△DHM≌△MBN(ASA),
∴DM=MN.
(3)结论:MN平分∠FMB成立.
证明:如图3中,在BO延长线上取OA=CF,
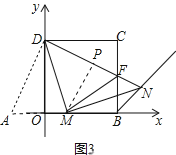
在△AOD和△FCD中,
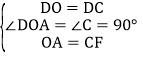 ,
,
∴△DOA≌△DCF,
∴AD=DF,∠ADO=∠CDF,
∵∠MDN=45°,
∴∠CDF+∠ODM=45°,
∴∠ADO+∠ODM=45°,
∴∠ADM=∠FDM,
在△DMA和△DMF中,
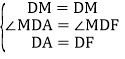 ,
,
∴△DMA≌△DMF,
∴∠DFM=∠DAM=∠DFC,
过M作MP⊥DN于P,则∠FMP=∠CDF,
由(2)可知∠NMF+∠FMP=∠PMN=45°,
∴∠NMB=∠MDO,∠MDO+∠CDF=45°,
∴∠NMB=∠NMF,即MN平分∠FMB.
故答案为:(1)(2+a,a);(2)证明见解析;(3)②MN平分∠FMB成立,证明见解析.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案科目:初中数学 来源: 题型:
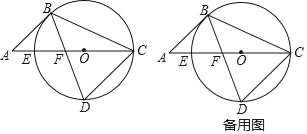
【题目】如图,已知CE是圆O的直径,点B在圆O上由点E顺时针向点C运动(点B不与点E、C重合),弦BD交CE于点F,且BD=BC,过点B作弦CD的平行线与CE的延长线交于点A.
(1)若圆O的半径为2,且点D为弧EC的中点时,求圆心O到弦CD的距离;
(2)当DFDB=CD2时,求∠CBD的大小;
(3)若AB=2AE,且CD=12,求△BCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各句判定矩形的说法![]()
![]() 对角线相等的四边形是矩形;
对角线相等的四边形是矩形;![]() 对角线互相平分且相等的四边形是矩形;
对角线互相平分且相等的四边形是矩形;![]() 有一个角是直角的四边形是矩形;
有一个角是直角的四边形是矩形;![]() 有四个角是直角的四边形是矩形;
有四个角是直角的四边形是矩形;![]() 四个角都相等的四边形是矩形;
四个角都相等的四边形是矩形;![]() 对角线相等,且有一个角是直角的四边形是矩形;是正确有几个
对角线相等,且有一个角是直角的四边形是矩形;是正确有几个![]()
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小聪和小明分别从相距30公里的甲、乙两地同时出发相向而行,小聪骑摩托车到达乙地后立即返回甲地,小明骑自行车从乙地直接到达甲地,函数图象y1(km)和y2(km)分别表示小聪离甲地的距离和小明离乙地的距离与已用时间t(h)之间的关系,如图所示.下列说法:①折线段OAB是表示小聪的函数图象y1,线段OC是表示小明的函数图象y2;②小聪去乙地和返回甲地的平均速度相同;③两人在出发80分钟后第一次相遇;④小明骑自行车的平均速度为15km/h,其中不正确的个数为( )
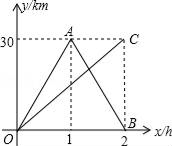
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1个单位长度的小正方形组成的格点图中,点A、B、C都是格点.
(1)点A坐标为______;点B坐标为______;点C坐标为______;
(2)画出△ABC关于原点对称的△A1B1C1;
(3)已知M(1,4),在x轴上找一点P,使|PM-PB|的值最大(写出过程,保留作图痕迹),并写出点P的坐标______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题:(1)如果 ![]() ,那么点
,那么点 ![]() 是线段
是线段 ![]() 的中点;(2)相等的两个角是对顶角;(3)直角三角形的两个锐角互余;(4)同位角相等;(5)两点之间,直线最短.其中真命题的个数有( )
的中点;(2)相等的两个角是对顶角;(3)直角三角形的两个锐角互余;(4)同位角相等;(5)两点之间,直线最短.其中真命题的个数有( )
A.1 个B.2 个C.3 个D.4 个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,点C、D在⊙O上,点E在⊙O外,∠EAC=∠D=60°.
(1)求∠ABC的度数;
(2)求证:AE是⊙O的切线;
(3)当BC=4时,求劣弧AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一方有难八方支援,某市政府筹集抗旱必需物资120吨打算运往灾区,现有甲、乙、丙三种车型可供选择,每辆车的运载能力和运费如下表所示:(假设每辆车均满载)

(1)若全部物资都用甲、乙两种车来运送,需运费8200元,则分别需甲、乙两种车各几辆?
(2)为了节约运费,该市政府共调用16辆甲、乙,丙三种车都参与运送物资,试求出有几种运送方案,哪种方案的运费最省?其费用是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
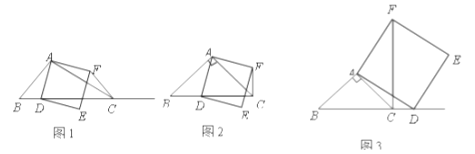
【题目】如图1,在![]() 中,
中,![]() 为锐角,点
为锐角,点![]() 为射线
为射线![]() 上一点,联结
上一点,联结![]() ,以
,以![]() 为一边且在
为一边且在![]() 的右侧作正方形
的右侧作正方形![]() .
.
(1)如果![]() ,
,![]() ,
,
①当点![]() 在线段
在线段![]() 上时(与点
上时(与点![]() 不重合),如图2,线段
不重合),如图2,线段![]() 所在直线的位置关系为 ,线段
所在直线的位置关系为 ,线段![]() 的数量关系为 ;
的数量关系为 ;
②当点![]() 在线段
在线段![]() 的延长线上时,如图3,①中的结论是否仍然成立,并说明理由;
的延长线上时,如图3,①中的结论是否仍然成立,并说明理由;
(2)如果![]() ,
,![]() 是锐角,点
是锐角,点![]() 在线段
在线段![]() 上,当
上,当![]() 满足什么条件时,
满足什么条件时,![]() (点
(点![]() 不重合),并说明理由.
不重合),并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com