
【题目】如图,∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE于![]() ,AD=4,BE=1.
,AD=4,BE=1.
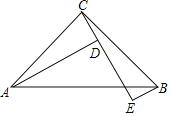
(1)求证:△ADC≌△CEB;
(2)求![]() 的长。
的长。
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】在探究两个三角形满足两边和其中一边的对角对应相等(“SSA”)是否能判定两个三角形全等时,我们设计不同情形进行探究:
(1)例如,当∠B 是锐角时,如图 ,BC=EF,∠B=∠E,在射线 EM 上有点 D,使 DF=AC,用尺规画出符合条件的点 D,则△ABC 和△DEF 的关系是( );
A.全等 B. 不全等 C. 不一定全等

我们进一步发现如果能确定这两个三角形的形状,那么“SSA”是成立的.
(2)例如,已知:如图,在锐角△ABC 和锐角△DEF 中,AC=DF,BC=EF,∠B=∠E. 求证:△ABC≌△DEF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC和△DEF(顶点为网格线的交点),以及过格点的直线l.
(1)将△ABC向右平移两个单位长度,再向下平移两个单位长度,画出平移后的三角形.
(2)画出△DEF关于直线l对称的三角形.
(3)填空:∠C+∠E= .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A的坐标为(-1,0),点B在直线![]() 上运动,当线段AB最短时,点B的坐标为( )
上运动,当线段AB最短时,点B的坐标为( )

A. (0,0) B. (![]() ,
,![]() ) C. (
) C. (![]() ,
,![]() ) D. (
) D. (![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,点![]() ,
,![]() ,
,![]() ,
,![]() 在一条直线上,
在一条直线上,![]() ,过
,过![]() ,
,![]() 分别作
分别作![]() ,
,![]() ,若
,若![]() .
.

(1)求证:![]() .
.
(2)若将![]() 的边
的边![]() 沿
沿![]() 方向移动得到图②,其他条件不变,(1)中结论是否仍然成立?请说明理由.
方向移动得到图②,其他条件不变,(1)中结论是否仍然成立?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应党的“文化自信”号召,某校开展了古诗词诵读大赛活动,现随机抽取部分同学的成绩进行统计,并绘制成如下的两个不完整的统计图,请结合图中提供的信息,解答下列各题:
(1)直接写出a的值,a= ,并把频数分布直方图补充完整.
(2)求扇形B的圆心角度数.
(3)如果全校有2000名学生参加这次活动,90分以上(含90分)为优秀,那么估计获得优秀奖的学生有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学问题:计算![]() (其中m,n都是正整数,且m≥2,n≥1).
(其中m,n都是正整数,且m≥2,n≥1).
探究问题:为解决上面的数学问题,我们运用数形结合的思想方法,通过不断地分割一个面积为1的正方形,把数量关系和几何图形巧妙地结合起来,并采取一般问题特殊化的策略来进行探究.
探究一:计算![]() .
.
第1次分割,把正方形的面积二等分,其中阴影部分的面积为![]() ;
;
第2次分割,把上次分割图中空白部分的面积继续二等分,阴影部分的面积之和为![]() +
+![]() ;
;
第3次分割,把上次分割图中空白部分的面积继续二等分,…;
…
第n次分割,把上次分割图中空白部分的面积最后二等分,所有阴影部分的面积之和为![]() +
+![]() +
+![]() +…+
+…+![]() ,最后空白部分的面积是
,最后空白部分的面积是![]() .
.
根据第n次分割图可得等式:![]() +
+![]() +
+![]() +…+
+…+![]() =1﹣
=1﹣![]() .
.

探究二:计算![]() +
+![]() +
+![]() +…+
+…+![]() .
.
第1次分割,把正方形的面积三等分,其中阴影部分的面积为![]() ;
;
第2次分割,把上次分割图中空白部分的面积继续三等分,阴影部分的面积之和为![]() +
+![]() ;
;
第3次分割,把上次分割图中空白部分的面积继续三等分,…;
…
第n次分割,把上次分割图中空白部分的面积最后三等分,所有阴影部分的面积之和为![]() +
+![]() +
+![]() +…+
+…+![]() ,最后空白部分的面积是
,最后空白部分的面积是![]() .
.
根据第n次分割图可得等式:![]() +
+![]() +
+![]() +…+
+…+![]() =1﹣
=1﹣![]() ,
,
两边同除以2,得![]() +
+![]() +
+![]() +…+
+…+![]() =
=![]() ﹣
﹣![]() .
.

探究三:计算![]() +
+![]() +
+![]() +…+
+…+![]() .
.
(仿照上述方法,只画出第n次分割图,在图上标注阴影部分面积,并写出探究过程)

解决问题:计算![]() +
+![]() +
+![]() +…+
+…+![]() .
.
(只需画出第n次分割图,在图上标注阴影部分面积,并完成以下填空)
根据第n次分割图可得等式:_________,
所以,![]() +
+![]() +
+![]() +…+
+…+![]() =________.
=________.
拓广应用:计算![]() +
+![]() +
+![]() +…+
+…+![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com