
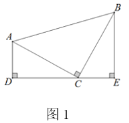
【题目】如图1 ,等腰直角三角形 ABC 中,∠ACB=90°,CB=CA,直线 DE 经过点 C,过 A 作 AD⊥DE 于点 D,过 B 作 BE⊥DE 于点 E,则△BEC≌△CDA,我们称这种全等模型为 “K 型全等”.(不需要证明)
(模型应用)若一次函数 y=kx+4(k≠0)的图像与 x 轴、y 轴分别交于 A、B 两点.
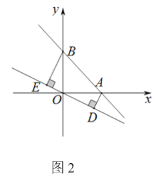
(1)如图 2,当 k=-1 时,若点 B 到经过原点的直线 l 的距离 BE 的长为 3,求点 A 到直线 l 的距离 AD 的长;
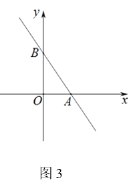
(2)如图 3,当 k=- ![]() 时,点 M 在第一象限内,若△ABM 是等腰直角三角形,求点
时,点 M 在第一象限内,若△ABM 是等腰直角三角形,求点
M 的坐标;
(3)当 k 的取值变化时,点 A 随之在 x 轴上运动,将线段 BA 绕点 B 逆时针旋转 90° 得到 BQ,连接 OQ,求 OQ 长的最小值.
【答案】(1)![]() ;(2)点M的坐标为(7,3)或(4,7)或(
;(2)点M的坐标为(7,3)或(4,7)或(![]() ,
,![]() );(3)OQ的最小值为4.
);(3)OQ的最小值为4.
【解析】
(1)先求出A、B两点的坐标,根据勾股定理即可求出OE的长,然后利用AAS证出△ADO≌△OEB,即可求出AD的长;
(2)先求出A、B两点的坐标,根据等腰直角三角形的直角顶点分类讨论,分别画出对应的图形,利用AAS证出对应的全等三角形即可分别求出点M的坐标;
(3)根据k的取值范围分类讨论,分别画出对应的图形,设点A的坐标为(x,0),证出对应的全等三角形,利用勾股定理得出OQ2与x的函数关系式,利用平方的非负性从而求出OQ的最值.
解:(1)根据题意可知:直线AB的解析式为y=-x+4
当x=0时,y=4;当y=0时,x=4
∴点A的坐标为(4,0)点B的坐标为(0,4)
∴OA=BO=4
根据勾股定理:OE= ![]()
∵∠ADO=∠OEB=∠AOB=90°
∴∠AOD+∠OAD=90°,∠AOD+∠BOE=90°
∴∠OAD=∠BOE
在△ADO和△OEB中

∴△ADO≌△OEB
∴AD= OE=![]()
(2)由题意可知:直线AB的解析式为y=![]() x+4
x+4
当x=0时,y=4;当y=0时,x=3
∴点A的坐标为(3,0)点B的坐标为(0,4)
∴OA=3,BO=4
①当△ABM是以∠BAM为直角顶点的等腰直角三角形时,AM=AB,过点M作MN⊥x轴于N
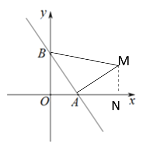
∵∠MNA=∠AOB=∠BAM=90°
∴∠MAN+∠AMN=90°,∠MAN+∠BAO=90°
∴∠AMN=∠BAO
在△AMN和△BAO中
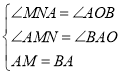
∴△AMN≌△BAO
∴AN=BO=4,MN=AO=3
∴ON=OA+AN=7
∴此时点M的坐标为(7,3);
②当△ABM是以∠ABM为直角顶点的等腰直角三角形时,BM=AB,过点M作MN⊥y轴于N

∵∠MNB=∠BOA=∠ABM=90°
∴∠MBN+∠BMN=90°,∠MBN+∠ABO=90°
∴∠BMN=∠ABO
在△BMN和△ABO中

∴△BMN≌△ABO
∴BN=AO=3,MN=BO=4
∴ON=OB+BN=7
∴此时点M的坐标为(4,7);
③当△ABM是以∠AMB为直角顶点的等腰直角三角形时,MA=MB,过点M作MN⊥x轴于N,MD⊥y轴于D,设点M的坐标为(x,y)
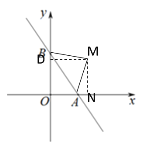
∴MD =ON=x,MN = OD =y,∠MNA=∠MDB=∠BMA=∠DMN=90°
∴BD=OB-OD=4-y,AN=ON-OA=x-3,∠AMN+∠DMA=90°,∠BMD+∠DMA=90°
∴∠AMN=∠BMD
在△AMN和△BMD中
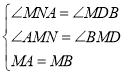
∴△AMN≌△BMD
∴MN=MD,AN=BD
∴x=y,x-3=4-y
解得:x=y=![]()
∴此时M点的坐标为(![]() ,
,![]() )
)
综上所述:点M的坐标为(7,3)或(4,7)或(![]() ,
,![]() ).
).
(3)①当k<0时,如图所示,过点Q作QN⊥y轴,设点A的坐标为(x,0)该直线与x轴交于正半轴,故x>0
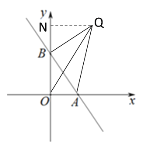
∴OB=4,OA=x
由题意可知:∠QBA=90°,QB=BA
∵∠QNB=∠BOA=∠ABQ=90°
∴∠QBN+∠BQN=90°,∠QBN+∠ABO=90°
∴∠BQN=∠ABO
在△BQN和△ABO中

∴△BQN≌△ABO
∴QN=OB=4,BN=OA=x
∴ON=OB+BN=4+x
在Rt△OQN中,OQ2=ON2+QN2=(4+x)2+42=(x+4)2+16,其中x>0
∴OQ2=(x+4)2+16>16
②当k>0时,如图所示,过点Q作QN⊥y轴,设点A的坐标为(x,0)该直线与x轴交于负半轴,故x<0

∴OB=4,OA=-x
由题意可知:∠QBA=90°,QB=BA
∵∠QNB=∠BOA=∠ABQ=90°
∴∠QBN+∠BQN=90°,∠QBN+∠ABO=90°
∴∠BQN=∠ABO
在△BQN和△ABO中

∴△BQN≌△ABO
∴QN=OB=4,BN=OA=-x
∴ON=OB-BN=4+x
在Rt△OQN中,OQ2=ON2+QN2=(4+x)2+42=(x+4)2+16,其中x<0
∴OQ2=(x+4)2+16≥16(当x=-4时,取等号)
综上所述:OQ2的最小值为16
∴OQ的最小值为4.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,直线y=kx+b(k≠0)与抛物线y=ax2(a≠0)交于A,B两点,且点A的横坐标是-2,点B的横坐标是3,则以下结论:
①抛物线y=ax2(a≠0)的图象的顶点一定是原点;
②x>0时,直线y=kx+b(k≠0)与抛物线y=ax2(a≠0)的函数值都随着x的增大而增大;
③AB的长度可以等于5;
④△OAB有可能成为等边三角形;
⑤当-3<x<2时,ax2+kx<b,
其中正确的结论是( )

A. ①②④ B. ①②⑤ C. ②③④ D. ③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
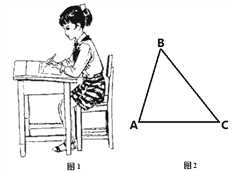
【题目】人写字时眼睛和笔端的距离超过30cm时则符合保护视力的要求.图1是一位同学的坐姿,把她的眼睛B、肘关节C和笔端A的位置关系抽象成图2的△ABC,BC=30cm,AC=22cm,∠ACB=530,她的这种坐姿符合保护视力的要求吗?请说明理由.(参考数据:sin530≈0.8,cos530≈0.6,tan530≈1.3)
查看答案和解析>>
科目:初中数学 来源: 题型:
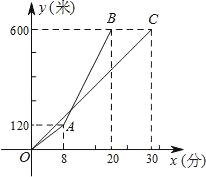
【题目】甲、乙两人沿同一路线登山,图中线段OC、折线OAB分别是甲、乙两人登山的路程y(米)与登山时间x(分)之间的函数图象.请根据图象所提供的信息,解答如下问题:
(1)求甲登山的路程与登山时间之间的函数关系式,并写出自变量x的取值范围;
(2)求乙出发后多长时间追上甲?此时乙所走的路程是多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE=90°.
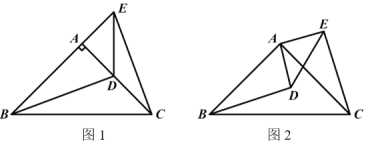
(1)当点D在AC上时,如下面图1,线段BD、CE有怎样的数量关系和位置关系?请直接写出结论,不需要证明.
(2)将下面图1中的△ADE绕点A顺时针旋转α角(0°<α<90°),如下图2,上述关系是否成立?如果成立请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,直线PQ垂直平分AC,与边AB交于E,连接CE,过点C作CF平行于BA交PQ于点F,连接AF.
(1)求证:△AED≌△CFD;
(2)求证:四边形AECF是菱形.
(3)若AD=3,AE=5,则菱形AECF的面积是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,P是对角线AC上任一点(不与A,C重合),连接BP,DP,过P作PE∥CD交AD于E,过P作PF∥AD交CD于F,连接EF.
(1)求证:△ABP≌△ADP;
(2)若BP=EF,求证:四边形EPFD是矩形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形![]() 是平行四边形,点
是平行四边形,点![]() 在
在![]() 边上运动(点
边上运动(点![]() 不与点
不与点![]() ,
,![]() 重合)
重合)
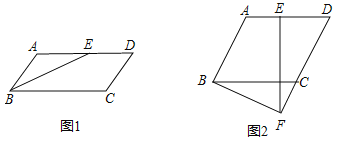
(1)如图1,当点![]() 运动到
运动到![]() 边的中点时,连接
边的中点时,连接![]() ,若
,若![]() 平分
平分![]() ,证明:
,证明:![]() ;
;
(2)如图2,过点![]() 作
作![]() 且交
且交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() .若
.若![]() ,
,![]() ,
,![]() ,在线段
,在线段![]() 上是否存在一点
上是否存在一点![]() ,使得四边形
,使得四边形![]() 是菱形?若存在,请说明当发
是菱形?若存在,请说明当发![]() ,点
,点![]() 分别在线段
分别在线段![]() ,
,![]() 上什么位置时四边形
上什么位置时四边形![]() 是菱形,并证明;若不存在,请说明理由.
是菱形,并证明;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com