
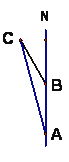
【题目】如图,上午9时,一条渔船从A出发,以12海里/时的速度向正北航行,11时到达B处,从A、B处望小岛C,测得∠NAC=15°,∠NBC=30°.若小岛周围12.3海里内有暗礁,问该渔船继续向正北航行有无触礁危险?
科目:初中数学 来源: 题型:
【题目】如图,在长方形![]() 中,
中,![]() 10厘米,
10厘米,![]() 6厘米,点
6厘米,点![]() 沿
沿![]() 边从点
边从点![]() 开始向点
开始向点![]() 以2厘米/秒的速度移动;点
以2厘米/秒的速度移动;点![]() 沿
沿![]() 边从点
边从点![]() 开始向点
开始向点![]() 以1厘米/秒的速度移动.如果
以1厘米/秒的速度移动.如果![]() 同时出发,用
同时出发,用![]() (秒)表示移动的时间.那么:
(秒)表示移动的时间.那么:
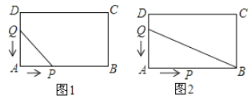
(1)如图1,用含![]() 的代数式表示
的代数式表示![]() 和
和![]() ,若线段
,若线段![]() ,求
,求![]() 的值.
的值.
(2)如图2,在不考虑点![]() 的情况下,连接
的情况下,连接![]() ,用含t的代数式表示△QAB的面积.
,用含t的代数式表示△QAB的面积.
(3)图2中,若△QAB的面积等于长方形![]() 的面积的
的面积的![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面文字,然后回答问题.
大家知道![]() 是无理数,而无理数是无限不循环小数,所以
是无理数,而无理数是无限不循环小数,所以![]() 的小数部分我们不可能全部写出来,由于
的小数部分我们不可能全部写出来,由于![]() 的整数部分是1,将
的整数部分是1,将![]() 减去它的整数部分,差就是它的小数部分,因此
减去它的整数部分,差就是它的小数部分,因此![]() 的小数部分可用
的小数部分可用![]() ﹣1表示.
﹣1表示.
由此我们得到一个真命题:如果![]() =x+y,其中x是整数,且0<y<1,那么x=1,y=
=x+y,其中x是整数,且0<y<1,那么x=1,y=![]() ﹣1.
﹣1.
请解答下列问题:
(1)如果![]() =a+b,其中a是整数,且0<b<1,那么a= ,b= ;
=a+b,其中a是整数,且0<b<1,那么a= ,b= ;
(2)如果﹣![]() =c+d,其中c是整数,且0<d<1,那么c= ,d= ;
=c+d,其中c是整数,且0<d<1,那么c= ,d= ;
(3)已知2+![]() =m+n,其中m是整數,且0<n<1,求|m﹣n|的值.
=m+n,其中m是整數,且0<n<1,求|m﹣n|的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设a、b、c是△ABC的三条边,关于x的方程x2+2![]() x+2c-a=0有两个相等的实数根,方程3cx+2b=2a的根为0.
x+2c-a=0有两个相等的实数根,方程3cx+2b=2a的根为0.
(1)求证:△ABC为等边三角形;
(2)若a,b为方程x2+mx-3m=0的两根,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
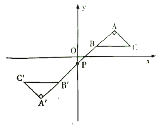
【题目】如图,在平面直角坐标系中,![]() 的顶点
的顶点![]() 在第一象限,点
在第一象限,点![]() 、
、![]() 的坐标分别为
的坐标分别为![]() 、
、![]() ,
,![]() ,
,![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() ,若
,若![]() 与
与![]() 关于点
关于点![]() 成中心对称,则点
成中心对称,则点![]() 的坐标为( )
的坐标为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠B+∠BCD=180°,∠B=∠D.

求证:∠E=∠DFE.
证明:∵∠B+∠BCD=180°( 已知 ),
∴AB∥CD ( )
∴∠B=_______( )
又∵∠B=∠D(已知 ),
∴∠D=_______( )
∴AD∥BE( )
∴∠E=∠DFE( )
查看答案和解析>>
科目:初中数学 来源: 题型:
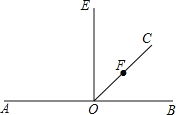
【题目】如图,O为直线AB上一点,F为射线OC上一点,OE⊥AB.
(1)用量角器和直角三角尺画∠AOC的平分线OD,画FG⊥OC,FG交AB于点G;
(2)在(1)的条件下,比较OF与OG的大小,并说明理由;
(3)在(1)的条件下,若∠BOC=40°,求∠AOD与∠DOE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划购进A,B两种型号的手机,已知每部A型号手机的进价比每部B型号手机进价多500元,每部A型号手机的售价是2500元,每部B型号手机的售价是2100元.
(1)若商场用50000元共购进A型号手机10部,B型号手机20部,求A、B两种型号的手机每部进价各是多少元?
(2)为了满足市场需求,商场决定用不超过7.5万元采购A、B两种型号的手机共40部,且A型号手机的数量不少于B型号手机数量的2倍.
①该商场有哪几种进货方式?
②该商场选择哪种进货方式,获得的利润最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com