
”¾ĢāÄæ”æŅŃÖŖ£ŗČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬”÷ABCŹĒÖ±½ĒČż½ĒŠĪ£¬”ĻACB£½90”ć£¬µćA£¬CµÄ×ų±ź·Ö±šĪŖA£Ø©3£¬0£©£¬C£Ø1£¬0£©£¬tan”ĻBAC£½![]() £®
£®
£Ø1£©Š“³öµćBµÄ×ų±ź£»
£Ø2£©ŌŚxÖįÉĻÕŅŅ»µćD£¬Į¬½ÓBD£¬Ź¹µĆ”÷ADBÓė”÷ABCĻąĖĘ£Ø²»°üĄØČ«µČ£©£¬²¢ĒóµćDµÄ×ų±ź£»
£Ø3£©ŌŚ£Ø2£©µÄĢõ¼žĻĀ£¬Čē¹ūµćP“ÓµćA³ö·¢£¬ŅŌ2cm/ĆėµÄĖŁ¶ČŃŲABĻņµćBŌĖ¶Æ£¬Ķ¬Ź±µćQ“ÓµćD³ö·¢£¬ŅŌ1cm/ĆėµÄĖŁ¶ČŃŲDAĻņµćAŌĖ¶Æ£®µ±Ņ»øöµćĶ£Ö¹ŌĖ¶ÆŹ±£¬ĮķŅ»øöµćŅ²ĖęÖ®Ķ£Ö¹ŌĖ¶Æ£®ÉčŌĖ¶ÆŹ±¼äĪŖt£®ĪŹŹĒ·ń“ęŌŚÕāŃłµÄtŹ¹µĆ”÷APQÓė”÷ADBĻąĖĘ£æČē“ęŌŚ£¬ĒėĒó³ötµÄÖµ£»Čē²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
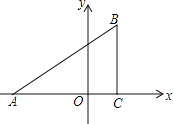
”¾“š°ø”æ£Ø1£©µćBµÄ×ų±źĪŖ£Ø1£¬3£©£»£Ø2£©µćDµÄ×ų±źĪŖ£Ø![]() £¬0£©£»£Ø3£©“ęŌŚ£¬µ±t£½
£¬0£©£»£Ø3£©“ęŌŚ£¬µ±t£½![]() s»ņ
s»ņ![]() sŹ±£¬”÷APQÓė”÷ADBĻąĖĘ£®
sŹ±£¬”÷APQÓė”÷ADBĻąĖĘ£®
”¾½āĪö”æ
£Ø1£©øł¾ŻÕżĒŠµÄ¶ØŅåĒó³öBC£¬µĆµ½µćBµÄ×ų±ź£»
£Ø2£©øł¾Ż”÷ABC”×”÷ADB£¬µĆµ½![]() =
=![]() £¬“śČė¼ĘĖćĒó³öAD£¬µĆµ½µćDµÄ×ų±ź£»
£¬“śČė¼ĘĖćĒó³öAD£¬µĆµ½µćDµÄ×ų±ź£»
£Ø3£©·Ö”÷APQ”×”÷ABD”¢”÷AQP”×”÷ABDĮ½ÖÖĒéæö£¬øł¾ŻĻąĖĘČż½ĒŠĪµÄŠŌÖŹĮŠŹ½¼ĘĖć¼“æÉ£®
½ā£ŗ£Ø1£©”ßA£Ø©3£¬0£©£¬C£Ø1£¬0£©£¬
”ąAC£½4£¬
”ß”ĻACB£½90”ć£¬tan”ĻBAC£½![]() £¬
£¬
”ą![]() £½
£½![]() £¬¼“
£¬¼“![]() £½
£½![]() £¬
£¬
½āµĆ£¬BC£½3£¬
”ąµćBµÄ×ų±źĪŖ£Ø1£¬3£©£»
£Ø2£©ČēĶ¼1£¬×÷BD”ĶBA½»xÖįÓŚµćD£¬
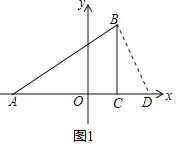
Ōņ”ĻACB£½”ĻABD£½90”ć£¬ÓÖ”ĻA£½”ĻA£¬
”ą”÷ABC”×”÷ADB£¬
”ą![]() £½
£½![]() £¬
£¬
ŌŚRt”÷ABCÖŠ£¬AB£½![]() £½
£½![]() £½5£¬
£½5£¬
”ą![]() £½
£½![]() £¬
£¬
½āµĆ£¬AD£½![]() £¬
£¬
ŌņOD£½AD©AO£½![]() £¬
£¬
”ąµćDµÄ×ų±źĪŖ£Ø![]() £¬0£©£»
£¬0£©£»
£Ø3£©“ęŌŚ£¬
ÓÉĢāŅāµĆ£¬AP£½2t£¬AQ£½![]() ©t£¬
©t£¬
µ±PQ”ĶABŹ±£¬PQ”ĪBD£¬
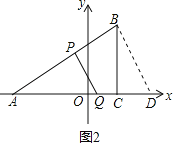
”ą”÷APQ”×”÷ABD£¬
”ą![]() £½
£½![]() £¬¼“
£¬¼“![]() £½
£½![]() £¬
£¬
½āµĆ£¬t£½![]() £¬
£¬
µ±PQ”ĶADŹ±£¬”ĻAQP£½”ĻABD£¬”ĻA£½”ĻA£¬
”ą”÷AQP”×”÷ABD£¬
”ą![]() £½
£½![]() £¬¼“
£¬¼“![]() £½
£½![]() £¬
£¬
½āµĆ£¬t£½![]() £¬
£¬
×ŪÉĻĖłŹö£¬µ±t£½![]() s»ņ
s»ņ![]() sŹ±£¬”÷APQÓė”÷ADBĻąĖĘ£®
sŹ±£¬”÷APQÓė”÷ADBĻąĖĘ£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æij±ö¹ŻÓŠ 50 øö·æ¼ä¹©ÓĪæĶ¾Ó×”£¬µ±Ćæøö·æ¼äµÄ¶Ø¼ŪĪŖĆæĢģ 160 ŌŖŹ±£¬·æ¼ä»įČ«²æ×”Āś£¬µ±Ćæøö·æ¼äĆæĢģµÄ¶Ø¼ŪĆæŌö¼Ó 10 ŌŖŹ±£¬¾Ķ»įÓŠŅ»øö·æ¼äæÕĻŠ£¬Čē¹ūÓĪæĶ¾Ó×”·æ¼ä£¬ ±ö¹ŻŠč¶ŌĆæøö·æ¼äĆæĢģÖ§³ö 20 ŌŖµÄø÷ÖÖ·ŃÓĆ£®ÉčĆæøö·æ¼äµÄ¶Ø¼ŪĪŖ x ŌŖŹ±£¬ĻąÓ¦µÄ×”·æŹżĪŖ y ¼ä£®
£Ø1£©Ēó y Óė x µÄŗÆŹż¹ŲĻµŹ½£»
£Ø2£©¶Ø¼ŪĪŖ¶ąÉŁŹ±±ö¹Żµ±ĢģĄūČó w ×ī“ó?²¢Ēó³öŅ»ĢģµÄ×ī“óĄūČó£»
£Ø3£©ČōĄĻ°å¾ö¶ØĆæ×”½ųČ„Ņ»¼ä·æ¾Ķ¾č³ö a ŌŖ£Øa”Ü30£©øųµ±µŲø£ĄūŌŗ£¬Ķ¬Ź±ŅŖ±£Ö¤·æ¼ä¶Ø¼Ū x ŌŚ 160 ŌŖÖĮ 350 ŌŖÖ®¼ä²Ø¶ÆŹ±£Ø°üĄØĮ½¶Ėµć£©£¬ĄūČó w Ėę x µÄŌö“ó¶ųŌö“ó£¬Ēó a µÄȔֵ·¶Ī§
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼ĖłŹ¾ĪŖ¶ž“ĪŗÆŹż![]() µÄĶ¼Ļó£¬ŌŚĻĀĮŠŃ”ĻīÖŠ“ķĪóµÄŹĒ£Ø £©
µÄĶ¼Ļó£¬ŌŚĻĀĮŠŃ”ĻīÖŠ“ķĪóµÄŹĒ£Ø £©
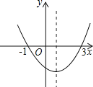
A. ![]()
B. ![]() Ź±£¬
Ź±£¬![]() Ėę
Ėę![]() µÄŌö“ó¶ųŌö“ó
µÄŌö“ó¶ųŌö“ó
C. ![]()
D. ·½³Ģ![]() µÄøłŹĒ
µÄøłŹĒ![]() £¬
£¬![]()
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬¶Ō½ĒĻßAC½«Õż·½ŠĪABCD·Ö³ÉĮ½øöµČŃüČż½ĒŠĪ£¬µćE£¬F½«¶Ō½ĒĻßACČżµČ·Ö£¬ĒŅAC£½15£¬µćPŌŚÕż·½ŠĪµÄ±ßÉĻ£¬ŌņĀś×ćPE+PF£½5![]() µÄµćPµÄøöŹżŹĒ£Ø””””£©
µÄµćPµÄøöŹżŹĒ£Ø””””£©
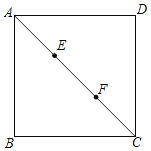
A.0B.4C.8D.16
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ![]() ÖŠ£¬
ÖŠ£¬![]() £¬
£¬ ![]() £¬µć
£¬µć![]() ĪŖ
ĪŖ![]() ±ßÉĻµÄ¶Æµć£Øµć
±ßÉĻµÄ¶Æµć£Øµć![]() ²»Óėµć
²»Óėµć![]() £¬
£¬![]() ÖŲŗĻ£©.ŅŌµć
ÖŲŗĻ£©.ŅŌµć![]() ĪŖ¶„µć×÷
ĪŖ¶„µć×÷![]() £¬ÉäĻß
£¬ÉäĻß![]() ½»
½»![]() ±ßÓŚµć
±ßÓŚµć![]() £¬¹żµć
£¬¹żµć![]() ×÷
×÷![]() ½»ÉäĻß
½»ÉäĻß![]() ÓŚ
ÓŚ![]() £¬Į¬½Ó
£¬Į¬½Ó![]() .
.
£Ø1£©ĒóÖ¤£ŗ![]() £»
£»
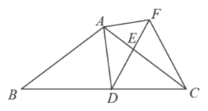
£Ø2£©µ±![]() Ź±£ØČēĶ¼£©£¬Ēó
Ź±£ØČēĶ¼£©£¬Ēó![]() µÄ³¤£»
µÄ³¤£»
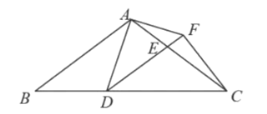
£Ø3£©µć![]() ŌŚ
ŌŚ![]() ±ßÉĻŌĖ¶ÆµÄ¹ż³ĢÖŠ£¬ŹĒ·ń“ęŌŚÄ³øöĪ»ÖĆ£¬Ź¹µĆ
±ßÉĻŌĖ¶ÆµÄ¹ż³ĢÖŠ£¬ŹĒ·ń“ęŌŚÄ³øöĪ»ÖĆ£¬Ź¹µĆ![]() £æČō“ęŌŚ£¬Ēó³ö“ĖŹ±
£æČō“ęŌŚ£¬Ēó³ö“ĖŹ±![]() µÄ³¤£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ.
µÄ³¤£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌĶĮĻĀĆęµÄ²ÄĮĻ£ŗ
°“ÕÕŅ»¶ØĖ³ŠņÅÅĮŠ×ŵÄŅ»ĮŠŹż³ĘĪŖŹżĮŠ£¬ŹżĮŠÖŠµÄĆæŅ»øöŹż½Š×öÕāøöŹżĮŠµÄĻī£®ÅÅŌŚµŚŅ»Ī»µÄŹż³ĘĪŖµŚŅ»Ļī£¬¼ĒĪŖ![]() £¬ÅÅŌŚµŚ¶žĪ»µÄŹż³ĘĪŖµŚ¶žĻī£¬¼ĒĪŖ
£¬ÅÅŌŚµŚ¶žĪ»µÄŹż³ĘĪŖµŚ¶žĻī£¬¼ĒĪŖ![]() £¬ŅĄ“ĖĄąĶĘ£¬ÅÅŌŚµŚnĪ»µÄŹż³ĘĪŖµŚnĻī£¬¼ĒĪŖ
£¬ŅĄ“ĖĄąĶĘ£¬ÅÅŌŚµŚnĪ»µÄŹż³ĘĪŖµŚnĻī£¬¼ĒĪŖ![]() £®ĖłŅŌ£¬ŹżĮŠµÄŅ»°ćŠĪŹ½æÉŅŌŠ“³É£ŗ
£®ĖłŅŌ£¬ŹżĮŠµÄŅ»°ćŠĪŹ½æÉŅŌŠ“³É£ŗ![]() £¬
£¬![]() £¬
£¬![]() £¬”£¬
£¬”£¬![]() £®
£®
Ņ»°ćµŲ£¬Čē¹ūŅ»øöŹżĮŠ“ÓµŚ¶žĻīĘš£¬ĆæŅ»ĻīÓėĖüĒ°Ņ»ĻīµÄ²īµČÓŚĶ¬Ņ»øö³£Źż£¬ÄĒĆ“ÕāøöŹżĮŠ½Š×öµČ²īŹżĮŠ£¬Õāøö³£Źż½Š×öµČ²īŹżĮŠµÄ¹«²ī£¬¹«²īĶس£ÓĆd±ķŹ¾£®Čē£ŗŹżĮŠ1£¬3£¬5£¬7£¬”ĪŖµČ²īŹżĮŠ£¬ĘäÖŠ![]() £¬
£¬![]() £¬¹«²īĪŖ
£¬¹«²īĪŖ![]() £®
£®
øł¾ŻŅŌÉĻ²ÄĮĻ£¬½ā“šĻĀĮŠĪŹĢā£ŗ
(1)µČ²īŹżĮŠ5£¬10£¬15£¬”µÄ¹«²īdĪŖ______£¬µŚ5ĻīŹĒ______£®
(2)Čē¹ūŅ»øöŹżĮŠ![]() £¬
£¬![]() £¬
£¬![]() £¬”£¬
£¬”£¬![]() ”£¬ŹĒµČ²īŹżĮŠ£¬ĒŅ¹«²īĪŖd£¬ÄĒĆ“øł¾Ż¶ØŅåæɵƵ½£ŗ
”£¬ŹĒµČ²īŹżĮŠ£¬ĒŅ¹«²īĪŖd£¬ÄĒĆ“øł¾Ż¶ØŅåæɵƵ½£ŗ![]() £¬
£¬![]() £¬
£¬![]() £¬”£¬
£¬”£¬![]() £¬”£®
£¬”£®
ĖłŅŌ![]() £¬
£¬
![]() £¬
£¬
![]() £¬
£¬
””£¬
ÓÉ“Ė£¬ĒėÄćĢīæÕĶź³ÉµČ²īŹżĮŠµÄĶØĻī¹«Ź½£ŗ![]() (______)d£®
(______)d£®
(3)![]() ŹĒ²»ŹĒµČ²īŹżĮŠ
ŹĒ²»ŹĒµČ²īŹżĮŠ![]() £¬
£¬![]() £¬
£¬![]() ”µÄĻī£æČē¹ūŹĒ£¬ŹĒµŚ¼øĻī£æ
”µÄĻī£æČē¹ūŹĒ£¬ŹĒµŚ¼øĻī£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĻóĘåŹĒĘåĄąŅęÖĒÓĪĻ·£¬ÖŠ¹śĻóĘåŌŚÖŠ¹śÓŠ×ÅČżĒ§¶ąÄźµÄĄśŹ·£¬ÓÉÓŚÓĆ¾ß¼ņµ„£¬Č¤Ī¶ŠŌĒ棬³ÉĪŖĮ÷ŠŠ¼«ĪŖ¹ć·ŗµÄĘåŅÕ»ī¶Æ£®ĄīæŗĶÕÅĆČĄūÓĆĻóĘåĘåÅĢŗĶĘå×Ó×öÓĪĻ·£®Ąī潫ĖÄƶĘå×Ó·“Ćę³ÆÉĻ·ÅŌŚĘåÅĢÉĻ£¬ĘäÖŠÓŠĮ½øö”°±ų”±”¢Ņ»øö”°Āķ”±”¢Ņ»øö”°Źæ”±£¬ÕÅĆČĖ껜“ÓÕāĖÄƶĘå×ÓÖŠĆžŅ»Ć¶Ęå×Ó£¬¼ĒĻĀÕżŗŗ×Ö£¬Č»ŗóŌŁ“ÓŹ£ĻĀµÄȿƶĘå×ÓÖŠĖ껜ƞŅ»Ć¶£®
£Ø1£©ĒóÕÅĆȵŚŅ»“ĪĆžµ½µÄĘå×ÓÕżĆęÉĻµÄŗŗ×ÖŹĒ”°±ų”±µÄøÅĀŹ£»
£Ø2£©ÓĪĻ·¹ę¶Ø£ŗČōÕÅĆČĮ½“ĪĆžµ½µÄĘå×ÓÖŠÓŠ”°Źæ”±£¬ŌņÕÅĆČŹ¤£»·ńŌņ£¬ĄīæŹ¤£®ĒėÄćÓĆŹ÷דĶ¼»ņĮŠ±ķ·ØĒóĄīæŹ¤µÄøÅĀŹ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬Ö±Ļßy=x+3ÓėxÖį½»ÓŚµćA£¬ÓėyÖį½»ÓŚµćB£¬Å×ĪļĻßy=a![]() +bx+c(a<0)¾¹żµćA£¬B£¬
+bx+c(a<0)¾¹żµćA£¬B£¬
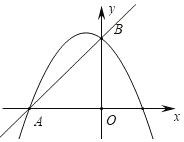
(1)Ēóa”¢bĀś×ćµÄ¹ŲĻµŹ½¼°cµÄÖµ£¬
(2)µ±x<0Ź±£¬Čōy=a![]() +bx+c(a<0)µÄŗÆŹżÖµĖęxµÄŌö“ó¶ųŌö“ó£¬ĒóaµÄȔֵ·¶Ī§£¬
+bx+c(a<0)µÄŗÆŹżÖµĖęxµÄŌö“ó¶ųŌö“ó£¬ĒóaµÄȔֵ·¶Ī§£¬
(3)ČēĶ¼£¬µ±a=1Ź±£¬ŌŚÅ×ĪļĻßÉĻŹĒ·ń“ęŌŚµćP£¬Ź¹”÷PABµÄĆ껿ĪŖ![]() ?Čō“ęŌŚ£¬ĒėĒó³ö·ūŗĻĢõ¼žµÄĖłÓŠµćPµÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£¬
?Čō“ęŌŚ£¬ĒėĒó³ö·ūŗĻĢõ¼žµÄĖłÓŠµćPµÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£¬
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Å×ĪļĻßy£½©![]() £Øx+1£©£Øx©9£©Óė×ų±źÖį½»ÓŚA”¢B”¢CČżµć£¬DĪŖ¶„µć£¬Į¬½įAC£¬BC£®µćPŹĒøĆÅ×ĪļĻßŌŚµŚŅ»ĻóĻŽÄŚÉĻµÄŅ»µć£®¹żµćP×÷yÖįµÄĘ½ŠŠĻß½»BCÓŚµćE£¬Į¬½įAP½»BCÓŚµćF£¬Ōņ
£Øx+1£©£Øx©9£©Óė×ų±źÖį½»ÓŚA”¢B”¢CČżµć£¬DĪŖ¶„µć£¬Į¬½įAC£¬BC£®µćPŹĒøĆÅ×ĪļĻßŌŚµŚŅ»ĻóĻŽÄŚÉĻµÄŅ»µć£®¹żµćP×÷yÖįµÄĘ½ŠŠĻß½»BCÓŚµćE£¬Į¬½įAP½»BCÓŚµćF£¬Ōņ![]() µÄ×ī“óÖµĪŖ_______£®
µÄ×ī“óÖµĪŖ_______£®
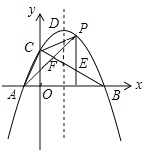
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com