
【题目】如图1,![]() 是
是![]() 的垂直平分线上一点,
的垂直平分线上一点,![]() 是
是![]() 轴上一点且
轴上一点且![]() .
.
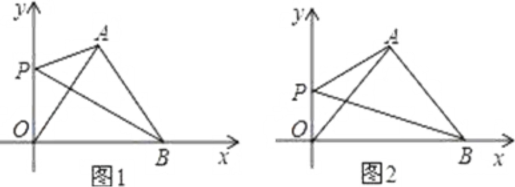
(1)若![]() ,
,![]() ,求点
,求点![]() 的坐标;
的坐标;
(2)在(1)的条件下,求证:![]() ;
;
(3)如图2,已知![]() ,求
,求![]() 的值.
的值.
【答案】(1)(0,2);(2)见解析(3)10.
【解析】
(1)根据垂直平分线性质可得OA=AB,根据∠AOB的大小可以求得∠OPB=60°,根据30°角所对直角边为斜边一半即可求得P点坐标;
(2)在PB上取一点E,使OP=OE,可证∠POA=∠EOB,可证△POA≌△EOB,可得PA=EB,即可解题;
(3)延长BA交y轴于点D,过A作AH⊥x轴,AE⊥y轴,可证BP=PD,即可求得PO+PB=OP+PD=OD即可解题.
解:(1)∵∠OPB=∠OAB,∠AOB=60°,
∴∠OPB=60°,
∴∠OBP=30°,
∵PB=4,
∴OP=2,
∴P点坐标为(0,2);
(2)在PB上取一点E,使OP=OE,

∵∠OPE=60°,
∴△POE是等边三角形,
∴∠POE=60°,PE=PO=OE,
∵∠AOB=60°,
∴∠POA=∠EOB
在△POA和△EOB中,
 ,
,
∴△POA≌△EOB(SAS),
∴PA=EB,
∴PB=PE+EB=PO+PA;
(3)延长BA交y轴于点D,过A作AH⊥x轴,AE⊥y轴;

∵OA=AB,
∴∠AOB=∠ABO,
∵∠ABO+∠ODB=∠AOB+∠AOD=90°,
∴∠AOD=∠ODB,
∴∠ODB=∠ABP,
∴AD=OA,BP=PD,
∴E为OD中点,
∵OE=AH=5,
∴PO+PB=PO+PD=OD=2OE=10.


科目:初中数学 来源: 题型:
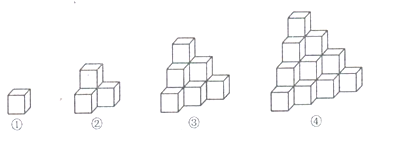
【题目】如图,用大小相同的小正方体从左至右摆放成几何体,若小正方体的棱长为1cm,则第①个几何体的表面积为6cm2,第②个几何体的表面积为18cm2,第③个几何体的表面积为36cm2,第④个几何体的表面积为60cm2,…,按照这样的规律,第n个几何体的表面积为________cm2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解方程:(1) ![]() ; (2)
; (2)![]() .
.
【答案】(1)x1 =1 ,x2=![]() ; (2) x1 =-1,x2=
; (2) x1 =-1,x2=![]() .
.
【解析】试题分析:
根据两方程的特点,使用“因式分解法”解两方程即可.
试题解析:
(1)原方程可化为: ![]() ,
,
方程左边分解因式得: ![]() ,
,
![]() 或
或![]() ,
,
解得: ![]() ,
, ![]() .
.
(2)原方程可化为: ![]() ,即
,即![]() ,
,
∴![]() ,
,
∴![]() 或
或![]() ,
,
解得: ![]() .
.
【题型】解答题
【结束】
20
【题目】已知x1,x2是关于x的一元二次方程x2-2(m+1)x+m2+5=0的两实根.
(1)若(x1-1)(x2-1)=28,求m的值;
(2)已知等腰△ABC的一边长为7,若x1,x2恰好是△ABC另外两边的边长,求这个三角形的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“某工厂用如图甲所示的长方形和正方形纸板做成如图乙所示的 A、B 两种长方体形状的无盖纸盒.现 有正方形纸板 120 张,长方形纸板 360 张,刚好全部用完,问能做成多少个 A 型盒子?”则下列结论 正确的个数是( )

①甲同学:设 A 型盒子个数为 x 个,根据题意可得: 4x 3 ![]() 360
360
②乙同学:设 B 型盒中正方形纸板的个数为 m 个,根据题意可得: 3 ![]() 4(120 m) 360
4(120 m) 360
③A 型盒 72 个
④B 型盒中正方形纸板 48 个
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
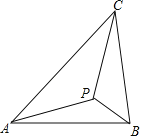
【题目】(2017湖南株洲)如图示,若△ABC内一点P满足∠PAC=∠PBA=∠PCB,则点P为△ABC的布洛卡点.三角形的布洛卡点(Brocard point)是法国数学家和数学教育家克洛尔(A.L.Crelle 1780﹣1855)于1816年首次发现,但他的发现并未被当时的人们所注意,1875年,布洛卡点被一个数学爱好者法国军官布洛卡(Brocard 1845﹣1922)重新发现,并用他的名字命名.问题:已知在等腰直角三角形DEF中,∠EDF=90°,若点Q为△DEF的布洛卡点,DQ=1,则EQ+FQ=( )
A. 5 B. 4 C. 3+![]() D. 2+
D. 2+![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com