
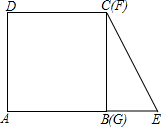
 如图,边长为4的正方形ABCD的边BC与直角边分别是2和4的Rt△GEF的边GF重合,正方形ABCD以每秒1个单位长度的速度沿GE向右匀速运动,当点A和点E重合时正方形停止运动.设正方形的运动时间为t秒,正方形ABCD与Rt△GEF重叠部分面积为S,则S关于t的函数图象为( )
如图,边长为4的正方形ABCD的边BC与直角边分别是2和4的Rt△GEF的边GF重合,正方形ABCD以每秒1个单位长度的速度沿GE向右匀速运动,当点A和点E重合时正方形停止运动.设正方形的运动时间为t秒,正方形ABCD与Rt△GEF重叠部分面积为S,则S关于t的函数图象为( )| A. | 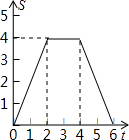 | B. | 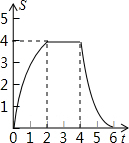 | C. | 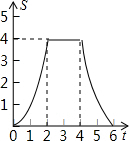 | D. | 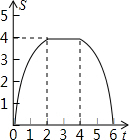 |
分析 分类讨论:当0≤t≤2时,BG=t,BE=2-t,运用△EBP∽△EGF的相似比可表示PB=4-2t,S为梯形PBGF的面积,则S=$\frac{1}{2}$(4-2t+4)•t=-t2+4t,其图象为开口向下的抛物线的一部分;当2<t≤4时,S=$\frac{1}{2}$FG•GE=4,其图象为平行于x轴的一条线段;当4<t≤6时,GA=t-4,AE=6-t,运用△EAP∽△EGF的相似比可得到PA=2(6-t),所以S为三角形PAE的面积,则S=(t-6)2,其图象为开口向上的抛物线的一部分.
解答 解:当0≤t≤2时,如图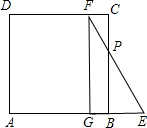 ,
,
BG=t,BE=2-t,
∵PB∥GF,
∴△EBP∽△EGF,
∴$\frac{PB}{FG}$=$\frac{EB}{EG}$,即$\frac{PB}{4}$=$\frac{2-t}{2}$,
∴PB=4-2t,
∴S=$\frac{1}{2}$(PB+FG)•GB=$\frac{1}{2}$(4-2t+4)•t=-t2+4t;
当2<t≤4时,S=$\frac{1}{2}$FG•GE=4;
当4<t≤6时,如图,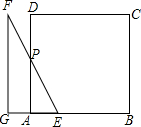
GA=t-4,AE=6-t,
∵PA∥GF,
∴△EAP∽△EGF,
∴$\frac{PA}{FG}$=$\frac{EA}{EG}$,即$\frac{PA}{4}$=$\frac{6-t}{2}$,
∴PA=2(6-t),
∴S=$\frac{1}{2}$PA•AE=$\frac{1}{2}$×2×(6-t)(6-t)
=(t-6)2,
综上所述,当0≤t≤2时,s关于t的函数图象为开口向下的抛物线的一部分;当2<t≤4时,s关于t的函数图象为平行于x轴的一条线段;当4<t≤6时,s关于t的函数图象为开口向上的抛物线的一部分.
故选B.
点评 本题考查了动点问题的函数图象:先根据几何性质得到与动点有关的两变量之间的函数关系,然后利用函数解析式和函数性质画出其函数图象,注意自变量的取值范围.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
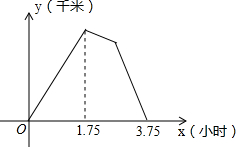 成渝两地山水相连风俗相通,人口、贸易往来频繁,“成渝高铁”的开通更是加速了成渝两地的“同城化进程”.已知两地相距350千米,现有一直达高铁往返于两城市之间,该高铁每次到达成都、重庆后均需停留1小时再重新出发.暑假期间,重庆市铁路局计划在同线路上临时加开一辆慢速直达旅行专列.在试运行期间,该旅行专列与高铁同时从重庆出发,在整个行驶过程中,两车均保持各自速度匀速行驶,经过3.75小时两车第一次相遇.已知两车之间的距离y(千米)与行驶时间x(小时)之间的部分函数关系如图所示,当两车第二次相遇时,该旅行专列共行驶了275千米.
成渝两地山水相连风俗相通,人口、贸易往来频繁,“成渝高铁”的开通更是加速了成渝两地的“同城化进程”.已知两地相距350千米,现有一直达高铁往返于两城市之间,该高铁每次到达成都、重庆后均需停留1小时再重新出发.暑假期间,重庆市铁路局计划在同线路上临时加开一辆慢速直达旅行专列.在试运行期间,该旅行专列与高铁同时从重庆出发,在整个行驶过程中,两车均保持各自速度匀速行驶,经过3.75小时两车第一次相遇.已知两车之间的距离y(千米)与行驶时间x(小时)之间的部分函数关系如图所示,当两车第二次相遇时,该旅行专列共行驶了275千米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知△ABC.
如图,已知△ABC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com