
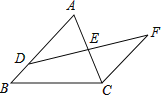
【题目】如图,点D是△ABC的边AB上一点,点E为AC的中点,过点C作CF∥AB交DE延长线于点F.
(1)求证:AD=CF.
(2)连接AF,CD,求证:四边形ADCF为平行四边形.
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,∠BAC=90°,分别以 AC 和 BC 为边向外作正方形 ACFG 和正方形 BCDE,过点 D 做 FC 的延长线的垂线,垂足为点 H.
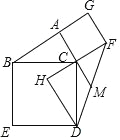
(1)求证:△ABC≌△HDC;
(2)连接 FD,交 AC 的延长线于点 M,若 AG=![]() ,tan∠ABC=
,tan∠ABC= ![]() ,求△FCM 的面积.
,求△FCM 的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李航想利用太阳光测量楼高.他带着皮尺来到一栋楼下,发现对面墙上有这栋楼的影子,针对这种情况,他设计了一种测量方案,具体测量情况如下:如示意图,李航边移动边观察,发现站到点E处时,可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠,且高度恰好相同.此时,测得李航落在墙上的影子高度CD=1.2m,CE=0.6m,CA=30m(点A、E、C在同一直线上).已知李航的身高EF是1.6m,请你帮李航求出楼高AB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 与
与![]() 、
、![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点.点
两点.点![]() 为线段
为线段![]() 的中点.过点
的中点.过点![]() 作直线
作直线![]() 轴于点
轴于点![]() .
.
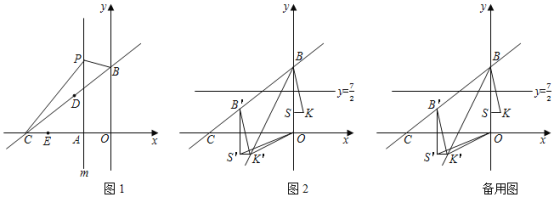
(1)直接写出![]() 的坐标;
的坐标;
(2)如图1,点![]() 是直线
是直线![]() 上的动点,连接
上的动点,连接![]() 、
、![]() ,线段
,线段![]() 在直线
在直线![]() 上运动,记为
上运动,记为![]() ,点
,点![]() 是
是![]() 轴上的动点,连接点
轴上的动点,连接点![]() 、
、![]() ,当
,当![]() 取最大时,求
取最大时,求![]() 的最小值;
的最小值;
(3)如图2,在![]() 轴正半轴取点
轴正半轴取点![]() ,使得
,使得![]() ,以
,以![]() 为直角边在
为直角边在![]() 轴右侧作直角
轴右侧作直角![]() ,
,![]() ,且
,且![]() ,作
,作![]() 的角平分线
的角平分线![]() ,将
,将![]() 沿射线
沿射线![]() 方向平移,点
方向平移,点![]() 、
、![]() ,
,![]() 平移后的对应点分别记作
平移后的对应点分别记作![]() 、
、![]() 、
、![]() ,当
,当![]() 的点
的点![]() 恰好落在射线
恰好落在射线![]() 上时,连接
上时,连接![]() ,
,![]() ,将
,将![]() 绕点
绕点![]() 沿顺时针方向旋转
沿顺时针方向旋转![]() 后得
后得![]() ,在直线
,在直线![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 为等腰三角形?若存在,请直接写出点
为等腰三角形?若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,圆柱形玻璃杯高为12cm、底面周长为18cm,在杯内离杯底4cm的点C
处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜的最
短距离为 ▲ cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
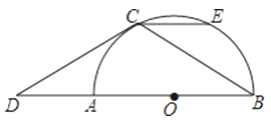
【题目】如图,AB是半圆O的直径,点C在半圆上,过点C的切线交BA的延长线于点D,CD=CB,CE∥AB交半圆于点E.
(1)求∠D的度数;
(2)求证:以点C,O,B,E为顶点的四边形是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践 问题情境:
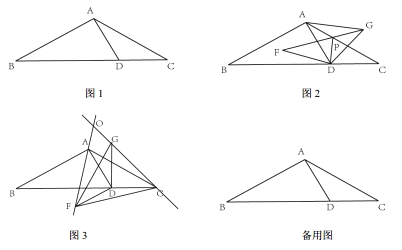
综合与实践课上,同学们以“三角形纸片的折叠与旋转“为主题展开数学活动,探究有关的数学问题.
动手操作:
已知:三角形纸片![]() 中,
中,![]() .将三角形纸片
.将三角形纸片![]() 按如下步骤进行操作:
按如下步骤进行操作:
第一步:如图1,折叠三角形纸片![]() ,使点
,使点![]() 与点
与点![]() 重合,然后展开铺平,折痕分别交
重合,然后展开铺平,折痕分别交![]() 于点
于点![]() ,连接
,连接![]() ,易知
,易知![]() .
.
第二步:在图1的基础上,将三角形纸片![]() 沿
沿![]() 剪开,得到
剪开,得到![]() 和
和![]() .保持
.保持![]() 的位置不变,将
的位置不变,将![]() 绕点
绕点![]() 逆时针旋转得到
逆时针旋转得到![]() (点
(点![]() 分别是
分别是![]() 的对应点),旋转角为
的对应点),旋转角为![]() 问题解决:
问题解决:
(1)如图2,小彬画出了旋转角![]() 时的图形,设线段
时的图形,设线段![]() 交于点
交于点![]() ,连接
,连接![]() .小彬发现
.小彬发现![]() 所在直线始终垂直平分线段
所在直线始终垂直平分线段![]() .请证明这一结论;
.请证明这一结论;
(2)如图3,小颖画出了旋转角![]() 时的图形,设直线
时的图形,设直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,连接
,连接![]() 判断此时
判断此时![]() 的形状,说明理由;
的形状,说明理由;
(3)在![]() 绕点
绕点![]() 逆时针旋转过程中,当
逆时针旋转过程中,当![]() 时,请直接写出
时,请直接写出![]() 两点间的距离.
两点间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
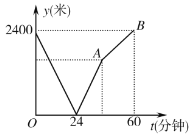
【题目】学校与图书馆在同一条笔直道路上,甲从学校去图书馆,乙从图书馆回学校,甲、乙两人都匀速步行且同时出发,乙先到达目的地.两人之间的距离![]() (米)与时间
(米)与时间![]() (分钟)之间的函数关系如图所示.其中说法正确的是( )
(分钟)之间的函数关系如图所示.其中说法正确的是( )
A.甲的速度是60米/分钟B.乙的速度是80米/分钟
C.点![]() 的坐标为
的坐标为![]() D.线段
D.线段![]() 所表示的函数表达式为
所表示的函数表达式为![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
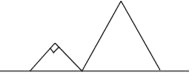
【题目】如图,直角边长为![]() 的等腰直角三角形与边长为3的等边三角形在同一水平线上,等腰直角三角形沿水平线从左向右匀速穿过等边三角形时,设穿过时间为t,两图形重合部分的面积为S,则S关于t的图象大致为( )
的等腰直角三角形与边长为3的等边三角形在同一水平线上,等腰直角三角形沿水平线从左向右匀速穿过等边三角形时,设穿过时间为t,两图形重合部分的面积为S,则S关于t的图象大致为( )
A. 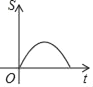 B.
B. 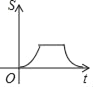
C. 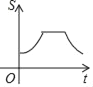 D.
D. 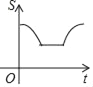
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com