
分析 (1)根据解一元一次不等式基本步骤:移项、合并同类项、系数化为1可得解集,依据大于向右、不包括该数用空心点在数轴上表示解集即可;
(2)根据解一元一次不等式基本步骤:去括号、移项、合并同类项、系数化为1可得不等式解集,依据小于向右,包括该数用实心点在数轴上表示解集即可.
解答 解:(1)移项,得:x-3x<-1-3,
合并同类项,得:-2x<-4,
系数化为1,得:x>2,
将解集表示在数轴上如图: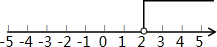
(2)去括号得:10-4x≥3x-18,
移项,得:-4x-3x≥-18-10,
合并同类项,得:-7x≥-28,
系数化为1,得:x≤4,
将解集表示在数轴上如图:
点评 本题主要考查解一元一次不等式的基本能力,严格遵循解不等式的基本步骤是关键,尤其需要注意不等式两边都乘以或除以同一个负数不等号方向要改变.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 如图,在菱形ABCD中,对角线AC和BD相交于点O,点E是BC的中点,连结AE,若
如图,在菱形ABCD中,对角线AC和BD相交于点O,点E是BC的中点,连结AE,若查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
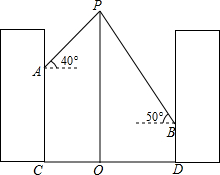 如图,某学校的两栋教学楼正中间有一个旗杆OP,旗杆底端O与两楼底部C、D在同一直线上,且OC=OD=10米,小明在图中左侧搂上点C的正上方A处测得旗杆顶端P的仰角为40°,小刚在图中右侧楼上点D的正上方B处测得旗杆顶端P的仰角为50°,侧得AC=8米,试求旗秆OP的长度和BD的长(参考数据:tan40°≈0.84,tan50°≈1.19,结果精确到0.1米)
如图,某学校的两栋教学楼正中间有一个旗杆OP,旗杆底端O与两楼底部C、D在同一直线上,且OC=OD=10米,小明在图中左侧搂上点C的正上方A处测得旗杆顶端P的仰角为40°,小刚在图中右侧楼上点D的正上方B处测得旗杆顶端P的仰角为50°,侧得AC=8米,试求旗秆OP的长度和BD的长(参考数据:tan40°≈0.84,tan50°≈1.19,结果精确到0.1米)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
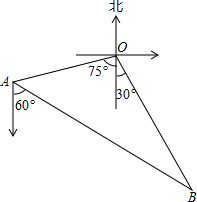 如图,编号为2307和2308的两艘海监船同时从港口O出发外出某岛海域巡航,2307海监船沿南偏西75°方向以每小时15$\sqrt{2}$海里的速度航行,2308海监船沿南偏东30°方向以每小时15海里的速度航行,航行1小时后,2307海监船在A处收到消息,2308海监船附近发现疑似敌舰,于是2307海监船迅速改变航向和速度,以匀速沿南偏东60°方向追赶2308海监船,正好在B处追上,2307海监船追赶2308海监船的速度为多少海里/时?
如图,编号为2307和2308的两艘海监船同时从港口O出发外出某岛海域巡航,2307海监船沿南偏西75°方向以每小时15$\sqrt{2}$海里的速度航行,2308海监船沿南偏东30°方向以每小时15海里的速度航行,航行1小时后,2307海监船在A处收到消息,2308海监船附近发现疑似敌舰,于是2307海监船迅速改变航向和速度,以匀速沿南偏东60°方向追赶2308海监船,正好在B处追上,2307海监船追赶2308海监船的速度为多少海里/时?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com