
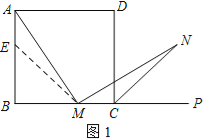
【题目】如图1,在正方形ABCD中,M是BC边(不含端点B、C)上任意一点,P是BC延长线上一点,N是∠DCP的平分线上一点.若∠AMN=90°,求证:AM=MN.
下面给出一种证明的思路,你可以按这一思路证明,也可以选择另外的方法证明.
证明:在边AB上截取AE=MC,连ME.
正方形ABCD中,∠B=∠BCD=90°,AB=BC.
∴∠NMC=180°—∠AMN—∠AMB
=180°—∠B—∠AMB
=∠MAB=∠MAE.
(下面请你完成余下的证明过程)
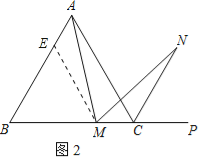
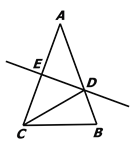
(2)若将(1)中的“正方形ABCD”改为“正三角形ABC”(如图2),N是∠ACP的平分线上一点,则当∠AMN=60°时,结论AM=MN是否还成立?请说明理由.
(3)若将(1)中的“正方形ABCD”改为“正![]() 边形ABCD…X”,请你作出猜想:当∠AMN=°时,结论AM=MN仍然成立.(直接写出答案,不需要证明)
边形ABCD…X”,请你作出猜想:当∠AMN=°时,结论AM=MN仍然成立.(直接写出答案,不需要证明)
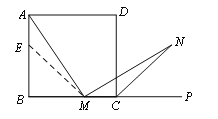
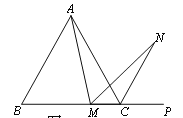
图1 图2
【答案】(1)证明见解析(2)仍然成立 (3) ![]()
【解析】试题分析:(1)要证明AM=MN,可证AM与MN所在的三角形全等,为此,可在AB上取一点E,使AE=CM,连接ME,利用ASA即可证明△AEM≌△MCN,然后根据全等三角形的对应边成比例得出AM=MN.
(2)同(1),要证明AM=MN,可证AM与MN所在的三角形全等,为此,可在AB上取一点E,使AE=CM,连接ME,利用ASA即可证明△AEM≌△MCN,然后根据全等三角形的对应边成比例得出AM=MN.
(3)由(1)(2)可知,∠AMN等于它所在的正多边形的一个内角即等于![]() 时,结论AM=MN仍然成立.
时,结论AM=MN仍然成立.
(1)证明:在边AB上截取AE=MC,连接ME.
∵正方形ABCD中,∠B=∠BCD=90°,AB=BC.
∴∠NMC=180°﹣∠AMN﹣∠AMB=180°﹣∠B﹣∠AMB=∠MAB=∠MAE,
BE=AB﹣AE=BC﹣MC=BM,
∴∠BEM=45°,∴∠AEM=135°.
∵N是∠DCP的平分线上一点,
∴∠NCP=45°,∴∠MCN=135°.
在△AEM与△MCN中,∠MAE=∠NMC,AE=MC,∠AEM=∠MCN,
∴△AEM≌△MCN(ASA),
∴AM=MN.
(2)解:结论AM=MN还成立
证明:在边AB上截取AE=MC,连接ME.
在正△ABC中,∠B=∠BCA=60°,AB=BC.
∴∠NMC=180°﹣∠AMN﹣∠AMB=180°﹣∠B﹣∠AMB=∠MAE,
BE=AB﹣AE=BC﹣MC=BM,
∴∠BEM=60°,∴∠AEM=120°.
∵N是∠ACP的平分线上一点,
∴∠ACN=60°,∴∠MCN=120°.
在△AEM与△MCN中,∠MAE=∠NMC,AE=MC,∠AEM=∠MCN,
∴△AEM≌△MCN(ASA),
∴AM=MN.
(3)解:若将(1)中的“正方形ABCD”改为“正n边形ABCD…X,则当∠AMN=![]() 时,结论AM=MN仍然成立.
时,结论AM=MN仍然成立.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:
【题目】计算:
①已知:a+![]() =1+
=1+![]() ,求a2+
,求a2+![]() 的值.
的值.
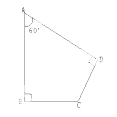
②如图,四边形ABCD中∠A=60°,∠B=∠D=90°,AB=2,CD=1,求四边形ABCD的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠B=∠C=∠EDF=α,BD=CF,BE=CD,则下列结论正确的是( )
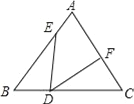
A. 2α+∠A=180° B. α+∠A=90° C. 2α+∠A=90° D. α+∠A=180°
查看答案和解析>>
科目:初中数学 来源: 题型:
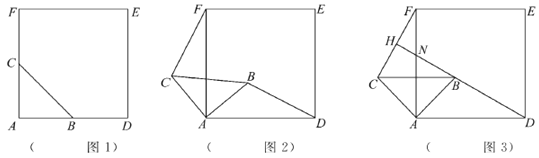
【题目】如图1,△ABC是等腰直角三角形,∠BAC= 90°,AB=AC,四边形ADEF是正方形,点B、C分别在边AD、AF上,此时BD=CF,BD⊥CF成立.
(1)当△ABC绕点A逆时针旋转θ(0°<θ<90°)时,如图2,BD=CF成立吗?若成立,请证明;若不成立,请说明理由.
(2)当△ABC绕点A逆时针旋转45°时,如图3,延长DB交CF于点H.
①求证:BD⊥CF;
②当AB=2,AD=3时,求线段DH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,正确的有( )
①平分弦的直径垂直于弦;
②三角形的三个顶点确定一个圆;
③圆内接四边形的对角相等;
④圆的切线垂直于过切点的半径;
⑤过圆外一点所画的圆的两条切线长相等.
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
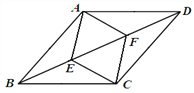
【题目】如图,点E、F为菱形ABCD对角线BD的三等分点.
(1)试判断四边形AECF的形状,并加以证明;
(2)若菱形ABCD的周长为52,BD为24,试求四边形AECF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AC的垂直平分线分别交AB、AC于点D、E.
(1)若∠A = 40°,求∠DCB的度数.
(2)若AE=4,△DCB的周长为13,求△ABC的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com