
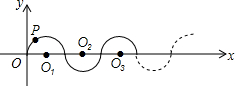
 如图所示,在平面直角坐标系中,半径均为1个单位长度的半圆O1、O2、O3,…组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒$\frac{π}{2}$个单位长度,则第2015秒时,点P的坐标是( )
如图所示,在平面直角坐标系中,半径均为1个单位长度的半圆O1、O2、O3,…组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒$\frac{π}{2}$个单位长度,则第2015秒时,点P的坐标是( )| A. | (2014,0) | B. | (2015,-1) | C. | (2015,1) | D. | (2016,0) |
分析 根据图象可得移动4次图象完成一个循环,从而可得出点A2015的坐标.
解答 解:半径为1个单位长度的半圆的周长为:$\frac{1}{2}×2π×1=π$,
∵点P从原点O出发,沿这条曲线向右运动,速度为每秒$\frac{π}{2}$个单位长度,
∴点P1秒走$\frac{1}{2}$个半圆,
当点P从原点O出发,沿这条曲线向右运动,运动时间为1秒时,点P的坐标为(1,1),
当点P从原点O出发,沿这条曲线向右运动,运动时间为2秒时,点P的坐标为(2,0),
当点P从原点O出发,沿这条曲线向右运动,运动时间为3秒时,点P的坐标为(3,-1),
当点P从原点O出发,沿这条曲线向右运动,运动时间为4秒时,点P的坐标为(4,0),
当点P从原点O出发,沿这条曲线向右运动,运动时间为5秒时,点P的坐标为(5,1),
当点P从原点O出发,沿这条曲线向右运动,运动时间为6秒时,点P的坐标为(6,0),
…,
∵2015÷4=503…3
∴P2015的坐标是(2015,-1),
故选:B.
点评 此题考查了点的规律变化,解答本题的关键是仔细观察图象,得到点的变化规律,解决问题.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题
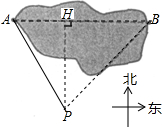 在一次测量活动中,同学们要测量某公园湖的码头A与它正东方向的亭子B之间的距离,如图.他们选择了与码头A、亭子B在同一水平面上的点P,在点P处测得码头A位于点P北偏西30°方向,亭子B位于点P北偏东43°方向;又测得点P与码头A之间的距离为400米.请你运用以上测得的数据求出码头A与亭子B之间的距离.(结果精确到1米,参考数据:$\sqrt{3}$≈1.7,tan43°≈0.93,sin43°≈0.68.)
在一次测量活动中,同学们要测量某公园湖的码头A与它正东方向的亭子B之间的距离,如图.他们选择了与码头A、亭子B在同一水平面上的点P,在点P处测得码头A位于点P北偏西30°方向,亭子B位于点P北偏东43°方向;又测得点P与码头A之间的距离为400米.请你运用以上测得的数据求出码头A与亭子B之间的距离.(结果精确到1米,参考数据:$\sqrt{3}$≈1.7,tan43°≈0.93,sin43°≈0.68.)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
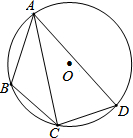 如图,在⊙O的内接四边形ABCD中,AB=3,AD=5,∠BAD=60°,点C为弧BD的中点,则AC的长是$\frac{8\sqrt{3}}{3}$.
如图,在⊙O的内接四边形ABCD中,AB=3,AD=5,∠BAD=60°,点C为弧BD的中点,则AC的长是$\frac{8\sqrt{3}}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
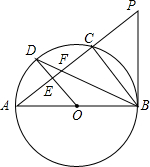 已知⊙O是以AB为直径的△ABC的外接圆,OD∥BC交⊙O于点D,交AC于点E,连接AD、BD,BD交AC于点F.
已知⊙O是以AB为直径的△ABC的外接圆,OD∥BC交⊙O于点D,交AC于点E,连接AD、BD,BD交AC于点F.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
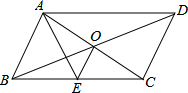 如图,?ABCD的对角线AC、BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=$\frac{1}{2}$BC,连接OE.下列结论:①∠CAD=30°;②S?ABCD=AB•AC;③OB=AB;④OE=$\frac{1}{4}$BC,成立的个数有( )
如图,?ABCD的对角线AC、BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=$\frac{1}{2}$BC,连接OE.下列结论:①∠CAD=30°;②S?ABCD=AB•AC;③OB=AB;④OE=$\frac{1}{4}$BC,成立的个数有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 为加强公民的节水意识,合理利用水资源.某市对居民用水实行阶梯水价,居民家庭每月用水量划分为三个阶梯,一、二、三级阶梯用水的单价之比等于1:1.5:2.如图折线表示实行阶梯水价后每月水费y(元)与用水量xm3之间的函数关系.其中线段AB表示第二级阶梯时y与x之间的函数关系
为加强公民的节水意识,合理利用水资源.某市对居民用水实行阶梯水价,居民家庭每月用水量划分为三个阶梯,一、二、三级阶梯用水的单价之比等于1:1.5:2.如图折线表示实行阶梯水价后每月水费y(元)与用水量xm3之间的函数关系.其中线段AB表示第二级阶梯时y与x之间的函数关系查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,∠C=90°,AC=2,点D在BC上,∠ADC=2∠B,AD=$\sqrt{5}$,则BC的长为( )
如图,在△ABC中,∠C=90°,AC=2,点D在BC上,∠ADC=2∠B,AD=$\sqrt{5}$,则BC的长为( )| A. | $\sqrt{3}$-1 | B. | $\sqrt{3}$+1 | C. | $\sqrt{5}$-1 | D. | $\sqrt{5}$+1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com