
 AE=4:3,坡长AB=10米,求小船C到岸边的距离CA的长?(参考数据:
AE=4:3,坡长AB=10米,求小船C到岸边的距离CA的长?(参考数据: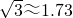 ,结果保留两位有效数字).
,结果保留两位有效数字). =
= ,
,
 (米).
(米).
 =CA+7,
=CA+7,

 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案科目:初中数学 来源: 题型:
 AE=4:3,坡长AB=10米,求小船C到岸边的距离CA的长?(参考数据:
AE=4:3,坡长AB=10米,求小船C到岸边的距离CA的长?(参考数据:| 3 |
查看答案和解析>>
科目:初中数学 来源:湖南省月考题 题型:解答题
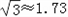 ,结果保留两位有效数字).
,结果保留两位有效数字).
查看答案和解析>>
科目:初中数学 来源: 题型:
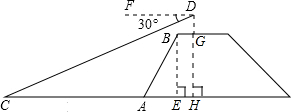
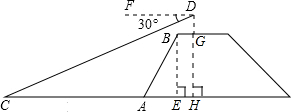
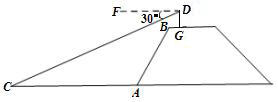
如图,张明站在河岸上的G点,看见河里有一只小船沿垂直于岸边的方向划过来,此时,他测得小船C的俯角是∠FDC=30°,若张明的眼睛与地面的距离是1.5米,BG=1米,BG平行于AC所在的直线,迎水坡的坡度i=4∶3,坡长AB=10米,求小船C到岸边的距离CA的长?(参考数据:![]() ,结果保留两位有效数字)
,结果保留两位有效数字)
查看答案和解析>>
科目:初中数学 来源:2010-2011学年湖南省长沙市麓山国际实验学校九年级(上)第三次月考数学试卷(解析版) 题型:解答题
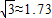 ,结果保留两位有效数字).
,结果保留两位有效数字).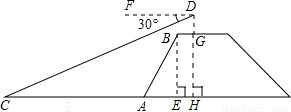
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com