

分析 过P作PE∥AB,构造同旁内角,通过平行线性质,可得∠APC=50°+60°=110°.
(1)过P作PE∥AD交CD于E,推出AD∥PE∥BC,根据平行线的性质得出∠α=∠DPE,∠β=∠CPE,即可得出答案;
(2)画出图形(分两种情况:①点P在BA的延长线上,②点P在AB的延长线上),根据平行线的性质得出∠α=∠DPE,∠β=∠CPE,即可得出答案.
解答 解:过P作PE∥AB,
∵AB∥CD,
∴PE∥AB∥CD,
∴∠APE=180°-∠A=50°,∠CPE=180°-∠C=60°,
∴∠APC=50°+60°=110°,
故答案为:110°;
(1)∠CPD=∠α+∠β,理由如下:
如图3,过P作PE∥AD交CD于E,
∵AD∥BC,
∴AD∥PE∥BC,
∴∠α=∠DPE,∠β=∠CPE,
∴∠CPD=∠DPE+∠CPE=∠α+∠β;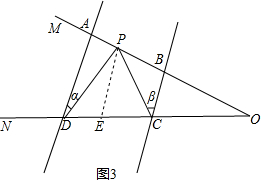
(2)当P在BA延长线时,∠CPD=∠β-∠α;
理由:如图4,过P作PE∥AD交CD于E,
∵AD∥BC,
∴AD∥PE∥BC,
∴∠α=∠DPE,∠β=∠CPE,
∴∠CPD=∠CPE-∠DPE=∠β-∠α;
当P在BO之间时,∠CPD=∠α-∠β.
理由:如图5,过P作PE∥AD交CD于E,
∵AD∥BC,
∴AD∥PE∥BC,
∴∠α=∠DPE,∠β=∠CPE,
∴∠CPD=∠DPE-∠CPE=∠α-∠β.
点评 本题考查了平行线的性质和判定的应用,主要考查学生的推理能力,解决问题的关键是作辅助线构造内错角以及同旁内角.


 高中必刷题系列答案
高中必刷题系列答案科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | $\sqrt{3}$ | D. | $-\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 序号项目 | 1 | 2 | 3 | 4 | 5 | 6 |
| 笔试成绩/分 | 85 | 92 | 84 | 90 | 84 | 80 |
| 面试成绩/分 | 90 | 88 | 86 | 90 | 80 | 85 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 甲户比乙户大 | B. | 乙户比甲户大 | ||
| C. | 甲、乙两户一样大 | D. | 无法确定哪一户大 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com