
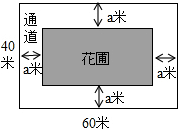
 如图,为美化校园环境,某校计划在一块长为60米,宽为40米的长方形空地上修建一个长方形花圃,并将花圃四周余下的空地修建成同样宽的通道,设通道宽为a米.
如图,为美化校园环境,某校计划在一块长为60米,宽为40米的长方形空地上修建一个长方形花圃,并将花圃四周余下的空地修建成同样宽的通道,设通道宽为a米.分析 (1)用含a的式子先表示出花圃的长和宽后利用其矩形面积公式列出式子即可;
(2)根据通道所占面积是整个长方形空地面积的$\frac{3}{8}$,列出方程进行计算即可;
(3)根据题意得:$\frac{40-2a}{60-2a}$=$\frac{40}{60}$,求得a值后即可判定是否满足要求.
解答 解:(1)由图可知,花圃的面积为(40-2a)(60-2a);
(2)由已知可列式:60×40-(40-2a)(60-2a)=$\frac{3}{8}$×60×40,
解以上式子可得:a1=5,a2=45(舍去),
答:所以通道的宽为5米;
(3)假设能满足要求,则$\frac{40-2a}{60-2a}$=$\frac{40}{60}$,
解得:a=0,
因为a=0不符合实际情况,所以不能满足其要求.
点评 本题考查了及一元二次方程的应用,解题的关键是表示出花圃的长和宽.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 亮亮同学是初三(甲)班的学生 | |
| B. | 2是质数 | |
| C. | 不知道亮亮今天数学作业做完了没有 | |
| D. | 如果a>b,a>c,那么b>c |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com