
如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B
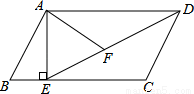
(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6 ,AF=4
,AF=4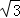 ,求AE的长.
,求AE的长.
(1)证明见解析;(2)6.
【解析】
试题分析:(1)利用对应两角相等,证明两个三角形相似△ADF∽△DEC;
(2)利用△ADF∽△DEC,可以求出线段DE的长度;然后在Rt△ADE中,利用勾股定理求出线段AE的长度.
试题解析:(1)证明:∵四边形ABCD是平行四变形,∴AB∥CD,AD∥BC,
∴∠C+∠B=180°,∠ADF=∠DEC.
∵∠AFD+∠AFE=180°,∠AFE=∠B,
∴∠AFD=∠C.
在△ADF与△DEC中,
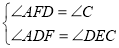
∴△ADF∽△DEC.
(2)【解析】
∵四边形ABCD是平行四边形,∴CD=AB=8.
由(1)知△ADF∽△DEC,
∴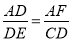
,∴DE=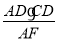 =12.
=12.
在Rt△ADE中,由勾股定理得:AE=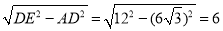 .
.
考点:1.相似三角形的判定与性质;2.勾股定理;3.平行四边形的性质.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源:2014-2015学年黑龙江省鸡西市八年级上学期期中考试数学试卷(解析版) 题型:选择题
有下列四个命题:①相等的角是对顶角;②两直线被第三条直线所截,同位角相等;③同位角互补两直线平行;④垂直于同一条直线的两条直线互相垂直。其中是假命题的有( )
A、4个 B、1个 C、2个 D、3个
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省九年级上学期期末模拟考试数学试卷(解析版) 题型:解答题
对于两个相似三角形,如果沿周界按对应点顺序环绕方向相同,那么称这两个三角形互为顺相似;如果沿周界按对应点顺序环绕的方向相反,那么称这两个三角形互为逆相似。例如:如图①,△ABC∽△A/B/C/,且沿周界ABCA与A/B/C/A/环绕的方向相同,因此△ABC与△A/B/C/互为顺相似;如图②△ABC∽△A/B/C/,且沿周界ABCA与A/B/C/A/环绕的方向相反,因此△ABC与△A/B/C/互为逆相似;

根据图Ⅰ、图Ⅱ、图Ⅲ满足的条件,可分别得下列三对相似三角形:
①△ADE与△ABC;②△FGH与△FNM③△OSK与△OQP.其中,互为顺相似的是 ;互为逆相似的是 。(填写所有符合要求的序号)
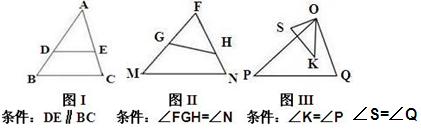
(2)如下图在锐角△ABC中,∠A<∠B<∠C,点P在△ABC的边上(不与A、B、C重合)过点P画直线截△ABC,使截得的一个三角形与△ABC互为逆相似,画出图形并说明截线满足的条件,不必说明理由。(请至少画出三种截法)

查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省九年级上学期期末模拟考试数学试卷(解析版) 题型:选择题
在三角形ABC中,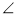 C为直角,sinA=
C为直角,sinA= ,则tanB 的值为( ).
,则tanB 的值为( ).
A. B.
B.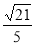 C.
C.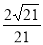 D.
D.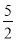
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省启东市滨海实验校共同体九年级上学期第二次质检数学试卷(解析版) 题型:解答题
如图,已知直线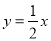 与双曲线
与双曲线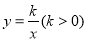 交于
交于 两点,且点
两点,且点 的横坐标为
的横坐标为 .
.
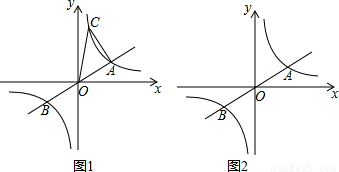
(1)求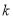 的值;
的值;
(2)若双曲线 上一点
上一点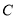 的纵坐标为8,求
的纵坐标为8,求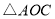 的面积;
的面积;
(3)过原点 的另一条直线
的另一条直线 交双曲线
交双曲线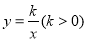 于
于 两点(
两点( 点在第一象限),若由点
点在第一象限),若由点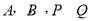 为顶点组成的四边形面积为
为顶点组成的四边形面积为 ,求点
,求点 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省启东市滨海实验校共同体九年级上学期第二次质检数学试卷(解析版) 题型:填空题
两个相似三角形一对对应边分别为35cm,14cm,它们的周长相差60cm,则较大三角形周长为 cm
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省启东市滨海实验校共同体九年级上学期第二次质检数学试卷(解析版) 题型:选择题
如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B→A的方向运动,设E点的运动时间为t秒(0≤t<6),连接DE,当△BDE是直角三角形时,t的值为( )
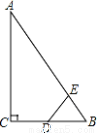
A.2 B.2.5或3.5 C.3.5或4.5 D.2或3.5或4.5
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省八年级上学期期中检测数学试卷(解析版) 题型:选择题
如图工人师傅砌门时,常用木条EF固定长方形门框ABCD,使其不变形,这样做的根据是( )
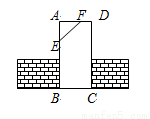
A、两点之间线段最短 B、两点确定一条直线
C、三角形具有稳定性 D、长方形的四个角都是直角
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com